На этом шаге мы рассмотрим первый, достаточно простой, сценарий.
Чтобы настроиться на работу, начнем для разминки с очень простого сценария.
Вновь представьте себе автомобиль, движущийся с постоянной скоростью 30 миль в час. Не больше и не меньше, а ровно 30 миль в час.
В приведенной ниже таблице указана скорость автомобиля в различные моменты времени с интервалом в полминуты.
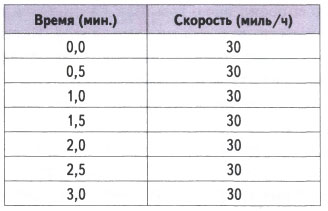
Следующий график представляет значения скорости в соответствующие моменты времени.

Как видите, скорость не изменяется с течением времени, и поэтому точки выстраиваются в прямую линию. Эта линия не идет ни вверх (увеличение скорости), ни вниз (уменьшение скорости), а остается на уровне 30 миль в час. В данном случае математическое выражение для скорости, которую мы обозначим как s, имеет следующий вид:
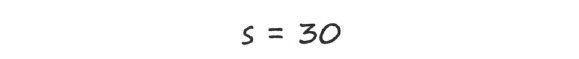
Если бы кто-то спросил нас о том, как изменяется скорость со временем, мы бы ответили, что она не изменяется. Скорость ее изменения равна нулю. Иными словами, скорость не зависит от времени. Зависимость в данном случае нулевая.
Мы только что выполнили одну из операций дифференциального исчисления! Эо не шутка!
Дифференциальное исчисление сводится к нахождению изменения одной величины в результате изменения другой. В данном случае нас интересует, как скорость изменяется со временем.
Вышеизложенное можно записать в следующей математической форме:
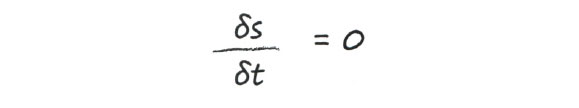
Что собой представляют эти символы? Считайте, что они означают "как скорость изменяется с изменением времени", или "как s зависит от t".
Таким образом, это выражение является компактной математической записью утверждения о том, что скорость не изменяется со временем. Другими словами, изменение времени не влияет на скорость. Зависимость скорости от времени нулевая. Именно это означает нуль в выражении. Обе величины полностью независимы. Ладно, ладно - мы все уже поняли!
В действительности эту независимость можно легко заметить, если вновь взглянуть на выражение для скорости s = 30. В нем вообще нет даже намека на время, т.е. в нем отсутствует любое проявление символа t. Поэтому, чтобы сказать, что ds / dt = 0, нам не потребуется никакое дифференциальное исчисление. Говоря языком математиков, "это следует из самого вида выражения".
Выражения вида ds / dt, определяющие степень изменения одной величины при изменении другой, называют производными. Для наших целей знание этого термина не является обязательным, но он вам может встретиться где-нибудь еще.
А теперь посмотрим, что произойдет, если надавить на педаль акселератора. Поехали!
На следующем шаге мы рассмотрим второй, более сложный, сценарий.
