На этом шаге мы рассмотрим более сложный сценарий.
Представьте себе все тот же автомобиль, движущийся со скоростью 30 миль в час. Вы надавили на педаль акселератора, и автомобиль набирает скорость. Вы удерживаете педаль нажатой, смотрите на показания спидометра и записываете их через каждые 30 секунд.
По прошествии 30 секунд скорость автомобиля составила 35 миль в час. Через минуту она возрастает до 40 миль в час. Через 90 секунд автомобиль ускоряется до 45 миль в час, а после двух минут автомобиль разгоняется до 50 миль в час. С каждой минутой скорость автомобиля увеличивается на 10 миль в час.
Эта информация сведена в представленной ниже таблице.
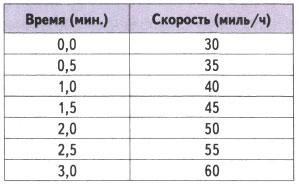
Визуализируем эти данные.
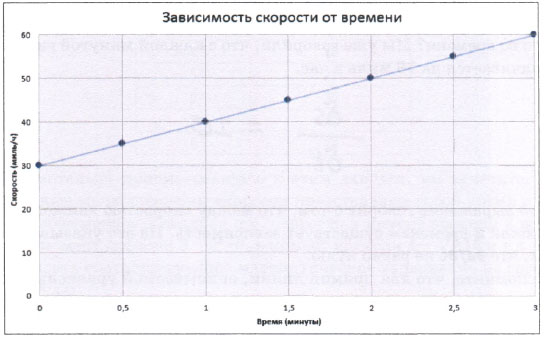
Как видите, увеличение скорости движения автомобиля с 30 до 60 миль в час происходит с постоянной скоростью изменения. Она действительно постоянна, поскольку приращение скорости за каждые полминуты остается одним и тем же, что приводит к прямолинейному графику скорости.
А что собой представляет выражение для скорости? В нулевой момент времени скорость равна 30 миль в час. Далее мы добавляем по 10 миль в час за каждую минуту. Таким образом, искомое выражение должно иметь следующий вид:
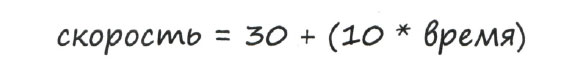
Перепишем его, используя символьные обозначения:
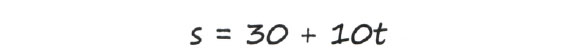
В этом выражении имеется константа 30. В нем также есть член (10 * время), который каждую минуту увеличивает скорость на 10 миль в час. Вы быстро сообразите, что 10 - это угловой коэффициент линии, график которой мы построили. Вспомните, что общая форма уравнения прямой линии имеет вид y = ax + b, где а - угловой коэффициент, или наклон, линии.
А как будет выглядеть выражение, описывающее изменение скорости во времени? Мы уже говорили, что с каждой минутой скорость увеличивается на 10 миль в час.
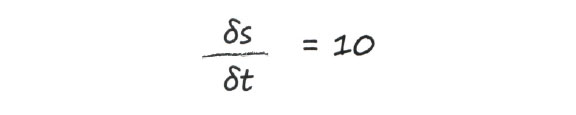
Это выражение говорит о том, что между скоростью движения автомобиля и временем существует зависимость. На это указывает тот факт, что ds / dt не равно нулю.
Вспомните, что для прямой линии, описываемой уравнением у = ах + b, наклон равен а, и поэтому наклон для прямой линии s = 30 + 10t должен быть равным 10.
Отличная работа! Мы уже успели охватить довольно много базовых элементов дифференциального исчисления, и это оказалось совсем несложно.
А теперь надавим на акселератор еще сильнее!
На следующем шаге мы рассмотрим еще один, третий, сценарий.
