На этом шаге мы рассмотрим еще один, третий сценарий.
Представьте, что мы начинаем поездку в автомобиле, нажав педаль акселератора почти до упора и удерживая ее в этом положении. Совершенно очевидно, что начальная скорость равна нулю, поскольку в первый момент автомобиль вообще не двигался.
Поскольку педаль акселератора нажата почти до упора, скорость движения будет увеличиваться не равномерно, а быстрее. Это означает, что скорость автомобиля уже не будет возрастать только на 10 миль в час каждую минуту. Само ежеминутное приращение скорости будет с каждой минутой увеличиваться, если педаль акселератора по-прежнему удерживается нажатой.
Предположим, что скорость автомобиля принимает в каждую минуту значения, приведенные в следующей таблице.
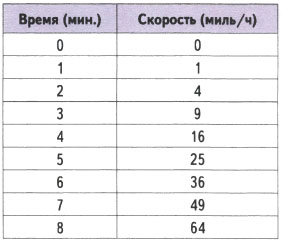
Внимательно присмотревшись к этим данным, вы заметите, что выбранные нами значения скорости представляют собой время в минутах, возведенное в квадрат, т.е. скорость в момент времени 2 равна 22=4, в момент времени 3 - 32=9, в момент времени 4 - 42=16 и т.д.
Записать соответствующее математическое выражение не составляет труда:
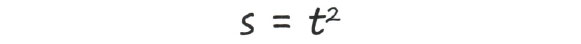
Да, мы отдаем себе отчет в том, что пример со скоростью автомобиля довольно искусственный, но он позволяет наглядно продемонстрировать, как мы можем использовать дифференциальное исчисление.
Представим табличные данные в виде графика, который позволит нам лучше понять характер изменения скорости автомобиля во времени.
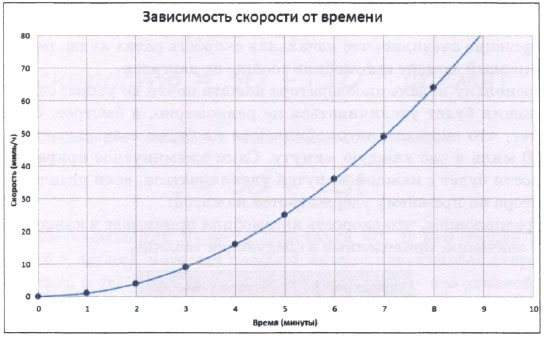
Как видите, со временем скорость автомобиля растет все интенсивнее. График уже не является прямой линией. Нетрудно сделать вывод, что вскоре скорость должна достигнуть очень больших значений. На 20-й минуте она должна была бы составить 400 миль в час, а на 100-й - целых 10000 миль в час!
Возникает интересный вопрос: как быстро изменяется скорость с течением времени? Другими словами, каково приращение скорости в каждый момент времени?
Это не то же самое, что спросить: а какова фактическая скорость в каждый момент времени? Ответ на этот вопрос нам уже известен, поскольку для него у нас есть соответствующее выражение: s = t2.
Мы же спрашиваем следующее: какова скорость изменения скорости автомобиля в каждый момент времени? Но что вообще это означает в нашем примере, в котором график оказался криволинейным?
Если вновь обратиться к двум предыдущим примерам, то в них скорость изменения скорости определялась наклоном графика зависимости скорости от времени. Когда автомобиль двигался с постоянной скоростью 30 миль в час, его скорость не изменялась, и поэтому скорость ее изменения была равна 0. Когда автомобиль равномерно набирал скорость, скорость ее изменения составляла 10 миль в час за минуту. Данный показатель имел одно и то же значение в любой момент времени. Он был равен 10 миль в час на второй, четвертой и даже на сотой минуте.
Можем ли мы применить те же рассуждения к криволинейному графику? Можем, но с этого момента нам следует немного сбавить темп, чтобы не спеша обсудить этот вопрос.
На следующем шаге мы рассмотрим применение дифференциального исчисления вручную.
