На этом шаге мы рассмотрим, как можно вручную произвести необходимые вычисления.
Присмотримся повнимательнее к тому, что происходит в конце третьей минуты движения. По прошествии трех минут с момента начала движения (t = 3) скорость (s) составит 9 миль в час. Сравним это с тем, что будет в конце шестой минуты движения. В этот момент скорость составит 36 миль в час, но мы знаем, что после этого автомобиль будет двигаться еще быстрее.
Мы также знаем, что в любой момент времени вслед за шестой минутой скорость будет увеличиваться быстрее, чем в эквивалентный момент времени, следующий за третьей минутой. Существует реальное различие в том, что происходит в моменты времени, соответствующие трем и шести минутам движения.
Представим все это в наглядной форме с помощью графика.

Вы видите, что в момент времени 6 минут наклон кривой круче, чем в момент времени 3 минуты. Оба наклона представляют искомую скорость изменения скорости движения. Очень важно, чтобы вы это поняли, потому повторим мысль в следующей формулировке: скорость изменения кривой в любой точке определяется ее наклоном в этой точке.
Но как измерить наклон линии, которая искривлена? С прямыми линиями все просто, а вот как быть с кривыми? Мы можем попытаться оценить наклон, прочертив прямую линию, так называемую касательную, которая лишь касается кривой (имеет с ней только одну общую точку) таким образом, чтобы иметь тот же наклон, что и кривая в данной точке. Именно так в действительности люди и поступали, пока не были изобретены другие способы.
Давайте испытаем этот приближенный простой способ хотя бы для того, чтобы лучше понять, к чему он приводит. На следующей иллюстрации представлен график скорости с касательной к кривой в точке, соответствующей шести минутам движения.
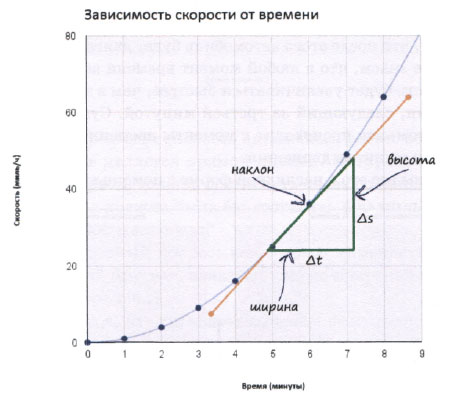
Из школьного курса математики нам известно, что для определения наклона, или углового коэффициента, следует разделить приращение вертикальной координаты на приращение горизонтальной координаты. На диаграмме приращение по вертикали (скорость) обозначено как Δs, а приращение по горизонтали (время) - как Δt. Символ Δ (читается "дельта") просто означает небольшое изменение. Поэтому Δt - это небольшое изменение t.
Наклон определяется отношением Δs / Δt. Мы можем выбрать для определения наклона любой треугольник и измерить длину его катетов с помощью линейки. В выбранном нами треугольнике приращение Δs оказалось равным 9,6, а приращение Δt - 0,8. Это дает следующую величину наклона.

Мы получили очень важный результат! Скорость изменения скорости в момент времени 6 минут составляет 12,0 миль в час за минуту.
Нетрудно заметить, что от способа, основанного на проведении касательной вручную и выполнении измерений с помощью линейки, вряд ли можно ожидать высокой точности. Поэтому мы должны обратиться к более совершенным методам.
На следующем шаге мы рассмотрим усовершенствованный способ применения дифференциального исчисления, допускающий автоматизацию.
