На этом шаге мы рассмотрим еще один способ применения диффернциального исчисления.
Взгляните на следующий график, на котором проведена другая прямая линия. Она не является касательной, поскольку имеет более одной общей точки с кривой. Но видно, что она в некотором смысле центрирована на моменте времени, соответствующем трем минутам.
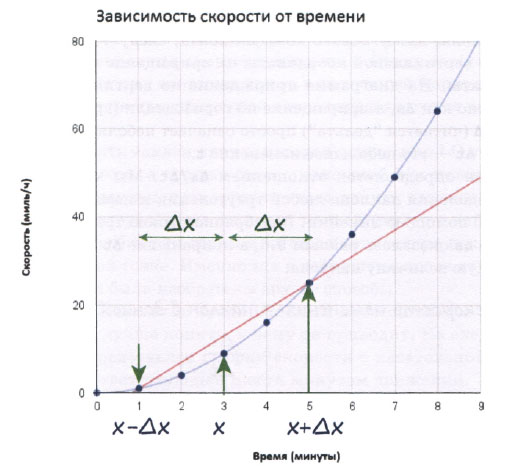
Связь этой прямой с моментом времени 3 минуты действительно существует. Для ее проведения были выбраны моменты времени до и после интересующего нас момента времени t = 3. В данном случае были выбраны точки, отстоящие от точки t = 3 на две минуты в большую и меньшую стороны, т.е. этим моментам времени соответствуют точки t = l и t = 5.
Используя математические обозначения, можно сказать, что Δх равно 2 минуты. Тогда выбранным нам точкам соответствуют координаты х - Δх и х + Δх. Вспомните, что символ Δ означает "небольшое изменение", поэтому Δх - это небольшое изменение х.
Зачем мы это делаем? Потерпите минутку - очень скоро все прояснится.
Если мы возьмем значения скорости в моменты времени х - Δх и х + Δх и проведем через соответствующие две точки прямую линию, то ее наклон будет примерно равен наклону касательной в средней точке х. Вернитесь к предыдущей иллюстрации и взгляните на эту прямую линию. Несомненно, ее наклон не совпадает в точности с наклоном истинной касательной в точке х, но мы исправим этот недостаток.
Вычислим наклон этой прямой. Мы используем прежний подход и рассчитаем наклон как отношение смещения точки по вертикали к смещению по горизонтали. Следующая иллюстрация проясняет, что в данном случае представляют собой эти смещения.
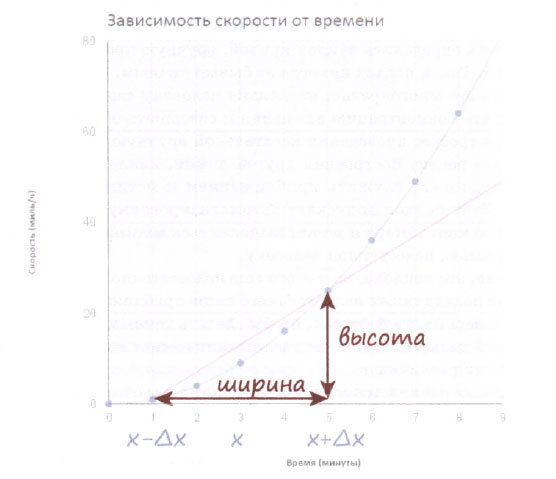
Смещение по вертикали - это разность между значениями скорости в точках х + Δх и х - Δх, соответствующих пяти минутам и одной минуте движения. Эти скорости нам известны: 52 = 25 и 12 = 1, поэтому разность составляет 24. Смещение по горизонтали - это просто расстояние между точками х + Δх и х - Δх, т.е. 5 - 1 = 4. Следовательно, имеем:

Таким образом, наклон прямой линии, являющейся приближением к касательной в точке t = 3 минуты, составляет 6 миль в час за минуту.
Сделаем паузу и осмыслим полученные результаты. Сначала мы попытались определить наклон кривой, вручную проведя касательную к ней. Такой подход никогда не бывает точным, и мы не можем повторять его многократно, поскольку человеку свойственно уставать, терять концентрацию внимания и совершать ошибки. Второй подход не требует проведения касательной вручную и вместо этого предлагает рецепт построения другой линии, наклон которой, по-видимому, может служить приближением к истинному наклону кривой. Этот подход допускает автоматизированную реализацию с помощью компьютера и может выполняться многократно с огромной скоростью, недоступной человеку.
Конечно, это неплохо, но и этого еще недостаточно!
Второй подход также является всего лишь приближенным. Можно ли его усовершенствовать так, чтобы сделать точным? В конце концов, нашей целью является точное математическое описание скорости изменения величин.
Вот здесь и начинается магия! Ппознакомим вас с одним из самых элегантных инструментов, разработанных математиками.
Что случится, если мы уменьшим величину смещения. Иными словами, что произойдет, если уменьшить Δх? Следующая иллюстрация демонстрирует несколько приближений в виде наклонных прямых, соответствующих уменьшению Δх.
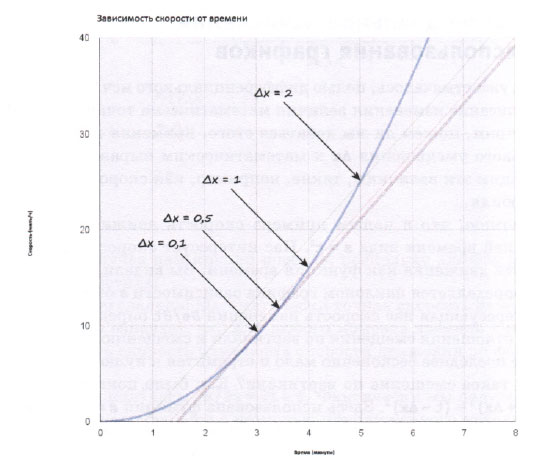
Мы провели линии для Δх = 2,0, Δх = 1,0, Δх = 0,5 и Δх = 0,1. Вы видите, что эти линии постепенно приближаются к интересующей нас точке х = 3. Нетрудно сообразить, что по мере уменьшения Δх прямые линии будут все более и более приближаться к истинной касательной.
При бесконечно малой величине Δх линия приблизится к истинной касательной на бесконечно малое расстояние. Это очень круто!
Идея постепенного улучшения первоначального приближенного решения путем уменьшения отклонений необычайно плодотворна. Она позволяет математикам решать задачи, непосредственное решение которых наталкивается на значительные трудности. При таком подходе к решению приближаются постепенно, словно крадучись, вместо того чтобы атаковать его прямо в лоб!
На следующем шаге мы рассмотрим дифференциальное исчисление без использования графиков.
