На этом шаге мы приведем математическое обоснование полученных результатов.
Как уже отмечалось, целью дифференциального исчисления является описание изменения величин математически точным способом. Посмотрим, можем ли мы добиться этого, применяя идею последовательного уменьшения Δх к математическим выражениям, определяющим эти величины, такие, например, как скорость движения автомобиля.
Напомню, что в нашем примере скорость движения является функцией времени вида s = t2. Нас интересует скорость изменения скорости движения как функция времени. Вы видели, что эта величина определяется наклоном графика зависимости s от t.
Интересующая нас скорость изменения ds / dt определяется величиной отношения смещения по вертикали к смещению по горизонтали, где последнее бесконечно мало и стремится к нулю.
Что такое смещение по вертикали? Как было показано раньше, это (t + Δх)2 - (t - Δх)2. Здесь использована функция s = t2, где t принимает значения, немного меньшие и немного большие, чем в интересующей нас точке. Это "немного" равно Δх.
Что такое смещение по горизонтали? Как вы видели раньше, это просто расстояние между точками (t + Δх) и (t - Δх), которое равно 2Δх.
Мы уже почти у цели:


В данном случае нам крупно повезло, поскольку алгебра необычайно все упростила.
Итак, мы это сделали! Математически точная скорость изменения ds / dt = 2t. Это означает, что для любого момента времени t мы можем вычислить скорость изменения скорости движения по формуле ds / dt = 2t.
При t = 3 мы получаем ds / dt = 2t = 6. Фактически мы подтвердили этот результат еще раньше с помощью приближенного метода. Для t = 6 получаем ds / dt = 2t = 12, что также согласуется с найденным ранее результатом.
А что насчет ста минут? В этом случае ds / dt = 2t = 200 миль в час за минуту. Это означает, что спустя сто минут от начала движения машина будет ускоряться со скоростью 200 миль в час за минуту.
Сделаем небольшую паузу и немного поразмышляем над величием и красотой того, что нам удалось сделать. Мы получили математическое выражение, с помощью которого можем точно определить скорость изменения скорости движения автомобиля в любой момент времени. При этом, в полном соответствии с нашими рассуждениями в начале приложения, мы видим, что эти изменения s действительно зависят от времени.
Нам повезло, что алгебра все упростила, но в силу простоты выражения s = t2 нам не представилась возможность проверить на практике идею устремления Δх к нулю. В связи с этим полезно рассмотреть другой пример, в котором скорость движения автомобиля описывается несколько более сложной формулой:
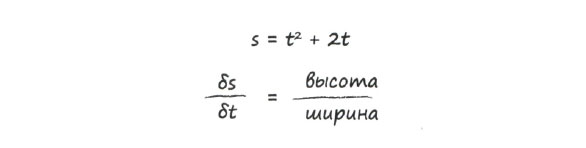
А что теперь означает вертикальное смещение? Это разность между скоростью s, рассчитанной в момент времени t + Δх, и скоростью s, рассчитанной в момент времени t - Δх. Найдем эту разность путем несложных вычислений: (t + Δх)2 + 2(t + Δх) - (t - Δх)2 - 2(t - Δх).
А что насчет горизонтального смещения? Это просто расстояние между точками (t + Δх) и (t - Δх), которое по-прежнему равно 2Δх:

Раскроем и упростим это выражение:
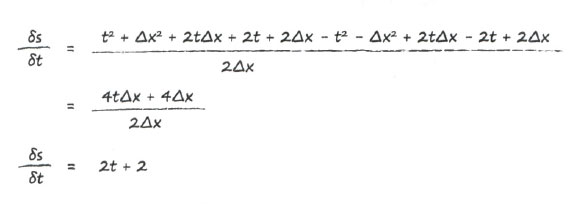
Это замечательный результат! К сожалению, алгебра и в этот раз немного перестаралась, упростив нам работу. Но этот пример не был напрасным, поскольку здесь уже вырисовывается закономерность, к которой мы еще вернемся.
Попробуем рассмотреть еще один, чуть более сложный, пример. Предположим, что скорость движения автомобиля описывается кубической функцией времени:

Раскроем и упростим это выражение:
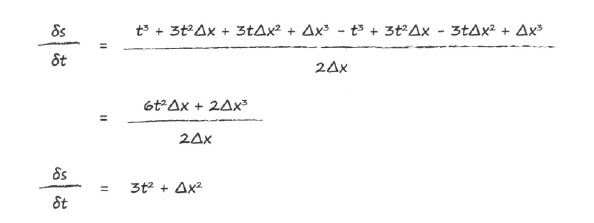
Это уже намного интереснее! Мы получили результат, содержащий Δх, тогда как раньше эти члены взаимно сокращались.
Вспомните, что корректное значение наклона получается лишь в том случае, если величина Δх уменьшается, становясь бесконечно малой.
А сейчас смотрите! Что произойдет с величиной Δх в выражении ds / dt = 3t2 + Δх2, если она становится все меньшей и меньшей? Она исчезнет! Если для вас это неожиданность, то представьте, что величина Δх очень мала. Напрягитесь и представьте, что она еще меньше. Потом представьте, что на самом деле она еще меньше... И этот процесс мысленного уменьшения Δх вы могли бы продолжать до бесконечности, устремляя ее к нулю. Поэтому давайте проявим решимость и сразу же перейдем к нулю без лишней суеты.
В результате мы получаем искомый математически точный ответ:

Это фантастический результат, и на этот раз он был получен с использованием мощного математического инструмента, что оказалось совсем несложным.
На следующем шаге мы рассмотрим закономерности.
