На этом шаге мы поговорим о том, какую роль играет тестирование при разработке приложений.

Тестирование - основной этап в любом процессе разработки программного обеспечения. В контексте данного мзложения его основная цель - обнаружение ошибок в коде. Таким образом, тестирование - это отладка разработанного программного обеспечения на различных экземплярах (различных входных параметрах) задачи с целью обнаружения неполадок. Начинающим программистам рекомендуется тестировать свой код, так как способность находить и исправлять ошибки (например, с помощью отладчика) является основным навыком программиста. Кроме того, тестирование - это ценнейший опыт по устранению ловушек и созданию более эффективного и надёжного кода.

Помимо проверки правильности начальных и рекурсивных условий, при тестировании рекурсивного кода программисты должны обращать особое внимание на возможные сценарии, приводящие к бесконечным рекурсиям. Обычно они возникают из-за недостаточных начальных условий или из-за ошибочных рекурсивных условий. Рассмотрим, например, функцию из примера 2.5.

Пример 2.5. Неправильный код для определения чётности неотрицательного целого числа n

1
2
3
4
5

def is_even_incorrect(n):
    if n == 0:
        return True
    else:
        return is_even_incorrect(n - 2)

Архив с файлом можно взять здесь.

Её цель - определить, является ли некоторое неотрицательное целое число n чётным. И начальные, и рекурсивные условия верны. Конечно, если число n - чётное, значит, (n - 2) - тоже чётное, и функция должна вернуть для обоих целых чисел одно и то же логическое значение. Однако is_even_incorrect() работает только для чётных чисел. Пусть f(n) обозначает is_even_incorrect(n), тогда вызов f(7) приведёт к следующей цепочке рекурсивных вызовов:

  f(7) → f(5) → f(3) → f(1) → f(-1) → f(-3) → ...     ,

что является бесконечной рекурсией, так как процесс не останавливается на начальном условии. То, что функция не имеет начального условия, возвращающего False, - это сигнал о том, что её нужно исправить (однако не все логические функции требуют двух начальных условий для возвращения True или False соответственно). В данном случае метод можно исправить, добавив в него ещё одно начальное условие. В примере 2.6 приведена функция, работающая для любого допустимого параметра (n ≥ 0).

Пример 2.6. Правильный код для определения чётности неотрицательного целого числа n

1
2
3
4
5
6
7

def is_even_correct(n):
    if n == 0:
        return True
    elif n == 1:
        return False
    else:
        return is_even_correct(n - 2)

Архив с файлом можно взять здесь.

Другой пример - функция из примера 2.7, которая для вычисления суммы первых n положительных целых чисел (S(n)) использует рекурсивное условие (2.1).

Пример 2.7. Ошибочное суммирование первых n положительных целых чисел, порождающее бесконечную рекурсию для большинства значений n

1
2
3
4
5

def sum_first_naturals_3(n):
    if n == 1:
        return 1
    else:
        return 2 * sum_first_naturals_3(n / 2) + (n / 2) ** 2

Архив с файлом можно взять здесь.

Оно - неполное и генерирует бесконечную рекурсию для значений n, не являющихся степенью двух. Во-первых, поскольку язык Python считает n вещественным числом, n/2 - тоже вещественное число. Поэтому если параметр n окажется нечётным в каком-нибудь рекурсивном вызове функции, то n/2 будет иметь дробную часть, и такими же будут аргументы последующих рекурсивных вызовов. Таким образом, алгоритм не остановится в начальном условии при n = 1 (которое является целым числом без дробной части) и продолжит вызывать функции с меньшими и меньшими аргументами. Например, пусть f(n) - это sum_ first_naturals_3(n). Вызов f(6) порождает следующую цепочку рекурсивных вызовов:

  f(6) → f(3) → f(1.5) → f(0.75) → f(0.375) → f(0.1875) → ...    ,

которая никогда не прервётся на начальном условии. Алгоритм работает лишь в одном случае - когда первый параметр n является степенью двух, поскольку каждое деление на два даёт чётное число, и по достижении n = 2 мы получим n = 1, для которого функция может, наконец, вернуть вместо очередного вызова самой себя конкретное значение.

Метод sum_first_naturals_3() работает неправильно, потому что его аргументы - вещественные числа. Таким образом, можно заменить вещественное деление целочисленным, как в примере 2.8, что сделает аргументы целочисленными и предотвратит бесконечную рекурсию.

Пример 2.8. Неполный код при сложении первых n положительных чисел

1
2
3
4
5

def sum_first_naturals_4(n):
    if n == 1:
        return 1
    else:
        return 2 * sum_first_naturals_4(n // 2) + (n // 2) ** 2

Архив с файлом можно взять здесь.

Однако и после этого функция все ещё будет работать неправильно для тех аргументов, которые не являются степенью двух. Проблема в том, что sum_first_naturals_4() - тоже неполная. В частности, несмотря на правильность рекурсивного условия, оно применимо только к чётным значениям n. На рисунке 1 показано, как в декомпозиции задачи получить рекурсивное условие S(n) = 2S((n - 1)/2) + ((n + 1)/2)² для нечётных n.

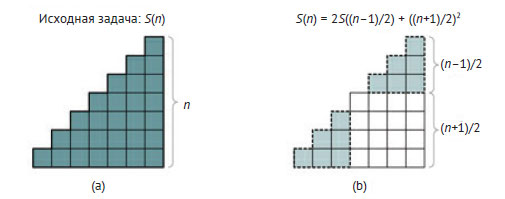
Рис.1. Схема декомпозиции суммы первых n положительных целых чисел S(n) на две подзадачи (примерно) в половину размера исходной для нечётных значений n

Следовательно, окончательная функция:

       1,                                   если n = 1,
S(n) = 2 * S(n / 2) + (n / 2)²,             если n > 1 и n - четное,
       2 * S((n - 1) / 2) + ((n + 1) / 2)², если n > 1 и n - нечетное,

а соответствующий код – в примере 2.9.

Пример 2.9. Сумма первых n положительных чисел с двумя подзадачами, размером (примерно) в половину исходной

1
2
3
4
5
6
7
8

def sum_first_naturals_5(n):
    if n == 1:
        return 1
    elif n % 2 == 0:
        return 2 * sum_first_naturals_5(n / 2) + (n / 2) ** 2  
    else:
        return 2 * sum_first_naturals_5((n - 1) / 2) \
               + ((n + 1) / 2) ** 2

Архив с файлом можно взять здесь.

При новом рекурсивном условии каждый, начиная с исходного, аргумент функции sum_first_naturals_5() также будет целым числом. В итоге замена вещественного деления (/) целочисленным (//) также приводит к правильному алгоритму.

На следующем шаге мы рассмотрим несколько примеров решения заданий.

Предыдущий шаг Содержание Следующий шаг