На этом шаге мы покажем, как можно использовать схемы для составления рекурсивных конструкций.
Часто полезно представить мыслительный процесс или "мысленную модель" вывода рекурсивных условий в виде схемы. На рисунке 1 приведена общая процедура рекурсивного мышления, когда декомпозиция задачи приводит к единственной, подобной ей подзадаче.
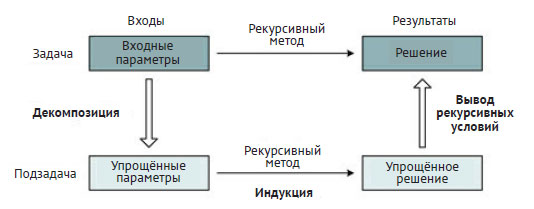
Рис.1. Общая схема обдумывания рекурсивных условий (когда декомпозиция задачи приводит к единственной, подобной ей подзадаче)
Процесс начинается с рассмотрения основного экземпляра задачи некоторого размера, определяемого входными параметрами, изображенными в верхнем левом блоке. Применение рекурсивного метода к этим параметрам должно привести к результатам, представленным в верхнем правом блоке. Отметим, что этот верхний ряд блоков - просто ещё один способ определения условий задачи. Для определения рекурсивных условий мы сначала выбираем некоторую декомпозицию, приводящую к меньшему экземпляру задачи. Новые, более простые параметры для подзадачи, подобной исходной, показаны в левом нижнем блоке. Рекурсивный вызов метода с этими параметрами должен, таким образом, выдать результаты (правый нижний блок), которые получаются применением условий задачи к более простым входным параметрам. И наконец, поскольку согласно методу индукции эти результаты следует считать правильными, мы выводим рекурсивные условия с учётом изменений или расширений, позволяющих добиться общего решения исходной задачи (верхний правый блок).
Для суммы первых n положительных целых чисел (S(n)) схема может быть такой:
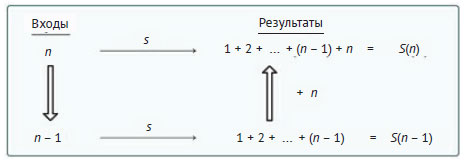
Для начала можно выбрать декомпозицию уменьшением размера задачи на единицу. Цель такой частной декомпозиции - выяснить, как можно получить S(n), изменив или расширив решение подзадачи S(n - 1). В этом случае легко видеть, что S(n) получается добавлением n к S(n - 1). Поэтому рекурсивное условие определяется как S(n) = S(n - 1) + n.
Важно понимать, что нам нужно всего лишь определить декомпозицию и установить, как получить результат исходной задачи, используя результат подзадачи. Следовательно, нам нужно думать только о процессах, обозначенных на схеме толстыми стрелками. С другой стороны, тонкие стрелки обозначают лишь итог решения отдельных экземпляров задачи (для различных входных параметров), который полностью определен условиями задачи. Отметим, что здесь не принимается никаких алгоритмических проектных решений об отношении между входом и выходом, поскольку они задаются условиями задачи.
Достоинство схемы на рисунке 1 в её общности: её можно применять к многочисленным задачам для получения рекурсивных решений. Поэтому объяснения большинства примеров опираются именно на неё. Конечно, не исключено применение и других графических представлений, таких как на рисунках 2 4 шага, 1 5 шага и 1 23 шага. Такая альтернативная визуализация особенно полезна, поскольку она показывает не только подзадачи, но и их связь с исходной задачей, что помогает объединять, расширять или изменять решения подзадач ради решения исходной задачи. Другими словами, они дают наглядное представление о том, как определить рекурсивные условия. Например, из схемы на рисунке 2 23 шага очевидно, что решение задачи заключается в добавлении n к результату подзадачи размера n - 1.
Конечно, более сложные схемы, специально приспособленные для отдельных задач, могут помочь найти различные декомпозиции, которые могли бы в конечном счете привести к более эффективным алгоритмам. Например, представление суммы первых n положительных целых чисел в виде блоков, выложенных треугольными пирамидами, как на рисунке 2 4 шага, позволяет легко вывести рекурсивные условия, когда размер подзадач равен примерно половине исходного. Во-первых, напомним, что задачу можно свести к подсчёту числа блоков в треугольной структуре. Кроме того, поскольку представление позволяет наложить поверх исходной задачи несколько подзадач (то есть меньшие треугольные структуры) одновременно, визуализация показывает, как "заполнить" бОльшую пирамиду меньшими. Поэтому схемы иллюстрируют, как получить рекурсивные условия путём сложения результатов (в данном случае - количество блоков) меньших подзадач. Например, на рисунке 2(c) 4 шага для получения результата исходной задачи нужно сложить результаты трёх подзадач размера n/2 и результат подзадачи размера n/2 - 1.
Тем не менее рекурсивное решение методом деления размера задачи S(n) пополам можно вывести и из общей схемы на рисунке 1. В этом случае мы имеем:

Однако здесь возникает вопрос: как (если это возможно) получить S(n) путём изменения или расширения S(n/2). Первая очевидная идея приводит к S(n) = S(n/2) + (n/2 + 1) + ... + n. И хотя она правильная, её реализация потребует использования либо цикла, либо другой рекурсивной функции для вычисления суммы последних n/2 членов. Отметим, что на этапе построения функции (S) получить сумму (n/2 + 1) + ... + n рекурсивным обращением к ней же невозможно, так как эта сумма не является экземпляром исходной задачи. Однако её можно преобразовать, например таким образом:
(n/2 + 1) + (n/2 + 2) + ... + (n/2 + n/2) = (n/2)2 + (1 + 2 + ... + n/2) = (n/2)2 + S(n/2).
Она не только упрощает выражение, но и содержит S(n/2), чем можно воспользоваться для получения гораздо более простого рекурсивного условия:
S(n) = S(n/2) + (n/2 + 1) + ... + n = S(n/2) + S(n/2) + (n/2)2 = 2S(n/2) + (n/2)2. (2.1)
Теперь общую схему можно изобразить следующим образом:
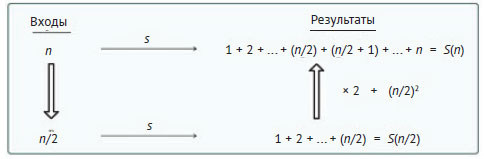
Из неё следует, что S(n) может быть получена умножением результата S(n/2) на 2 и добавлением к нему (n/2)2. Хотя декомпозиция задачи приводит к единственной подзадаче (S(n/2)), этот пример показывает, что для решения исходной задачи результат её подзадачи может использоваться несколько раз. В данном случае можно считать, что рекурсивное условие использует S(n/2) дважды.
Это рекурсивное условие можно также получить из схемы на рисунке 2, где S(n) изображается в виде треугольной пирамиды и тем самым доказывается, что S(n) = 2S(n/2) + (n/2)2.
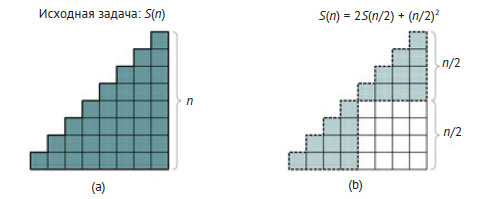
Рис.2. Схема декомпозиции задачи о сумме первых n положительных целых чисел S(n), использующая две подзадачи в половину размера исходной
Естественность такой схемы, где решение задачи сводится к сложению блоков, облегчает получение рекурсивных условий.
На следующем шаге мы рассмотрим конкретные экземпляры задачи.
