На этом шаге мы рассмотрим это понятие.

    Арифметическая прогрессия - это числовая последовательность s_i (i = 0, 1, 2, ...), каждый член которой больше предыдущего на заданную константу d (которая может быть отрицательной). Иными словами, s_i = s_i-1 + d для i > 0, что является рекурсивным определением. Элементы арифметической прогрессии можно также определить нерекурсивно следующим образом:

  si = si-1 + d = si-2 + 2 * d = ... = s0 + i * d   (3.6)

    Хотя теоретически арифметическая прогрессия бесконечна, а её сумма равна

   ∞            
   ∑ si    ,
  i=0            

   ∞            
   ∑ si    ,
  i=m            

    При анализе эффективности рекурсивных и итерационных алгоритмов часто используется сумма первых n положительных целых чисел S(n), под которой подразумевается частичная сумма (n элементов) арифметической прогрессии (s₀ = 1 и d = 1):

          n-1     n-1               n-1          n-1    n-1        n-1     n            
   S(n) = ∑ si = ∑ (s0 + i * d) = ∑ (1 + i) = ∑ 1 + ∑ i = n + ∑ i = ∑ i
          i=0    i=0                i=0          i=0    i=0        i=0    i=1

    Как показано в 9 шаге, результат этой суммы можно представить в виде квадратного полинома от n (1.12). Эту формулу просто вывести, сложив две суммы S(n), одна из которых суммируется в возрастающем порядке, а другая - в убывающем. Тогда из полученного результата следует, что 2S(n) = n(n + 1), поскольку в правой части равенства мы имеем n слагаемых, каждое из которых равно n + 1. После деления правой части на 2 получаем

          n            
   S(n) = ∑ i = n * (n + 1) / 2        .
         i=1 

    Графическая иллюстрация этой интересной идеи приведена на рисунке 1, где S(n) - площадь треугольной "лесенки" из квадратиков размера 1×1.

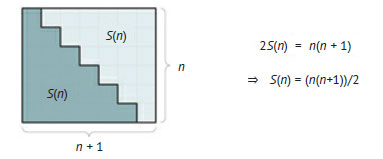
Рис.1. Графический способ вывода формулы для суммы S(n) первых n положительных целых чисел

    Две такие "лесенки" можно соединить так, чтобы получился прямоугольник размером n×(n + 1). Из чего следует, что площадь S(n) каждой "лесенки" равна n(n + 1)/2.

    Подобную формулу можно получить и для частичной суммы n членов арифметической прогрессии (s_i = s_i-1 + d для некоторого начального значения s₀)

          n-1            
   S(n) = ∑ si = n * (s0 + sn-1) / 2        .
          i=0 

    На следующем шаге мы рассмотрим геометрическую прогрессию.

Предыдущий шаг Содержание Следующий шаг