На этом шаге мы рассмотрим особенности реализации этого алгоритма.

Алгоритм quickselect, также разработанный Чарльзом Хоаром, - это алгоритм поиска выбором, основанный на схеме разбиения Хоара. В частности, он находит в несортированном списке k-е наименьшее число (называемое также статистикой k-го порядка). Пусть экземпляр задачи определяется входными параметрами - числовым списком а, нижним и верхним индексами внутри списка и положительным целочисленным значением k. Тогда алгоритм должен найти k-е наименьшее число в заданном подсписке. Размер задачи - длина подсписка. Наименьшие экземпляры задачи соответствуют спискам из одного элемента. Поэтому начальное условие выполняется, когда нижний и верхний индексы совпадают, а метод просто возвращает этот единственный элемент списка.

Для больших списков метод сначала применяет схему разбиения Хоара, который делит список на три подсписка и упорядочивает каждый из них. Первый подсписок содержит элементы, не большие выбранного опорного элемента списка. За ним следует подсписок, состоящий только из одного опорного элемента. И наконец, третий подсписок содержит элементы, бОльшие опорного.

Пусть i_p обозначает индекс опорного элемента. Поскольку функция, реализующая схему разбиения Хоара, возвращает i_p, можно проверить, равен ли он k - 1 (так как индексы начинаются с 0, а j-й элемент находится в позиции j - 1). Если это так, то опорный элемент - k-й наименьший элемент в а, и метод заканчивается на этом начальном условии. Этот сценарий приведён на рисунке 1(a).

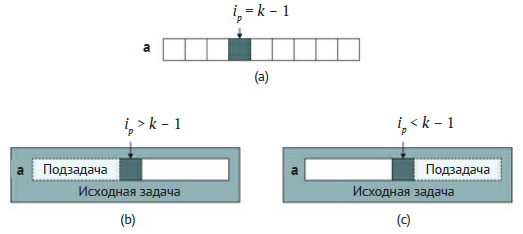
Рис.1. Начальное условие и декомпозиция задачи, используемые алгоритмом quickselect

В рекурсивном условии алгоритм уменьшает размер задачи за счёт перехода либо к левому от опорного элемента подсписку, либо к правому. Если i_p > k - 1, то позиция искомого элемента будет меньше i_p, алгоритм может сосредоточиться на подсписке слева от опорного, как показано на рисунке 1(b). Иначе, если i_p < k - 1, алгоритм продолжает решать подзадачу в правом от опорного подсписке, как показано на рисунке 1(c). В заключение приведём пример 5.14 с реализацией хвостовой рекурсивной функции.

Пример 5.14. Хвостовой рекурсивный алгоритм quickselect

1
2
3
4
5
6
7
8
9
10
11
12

def quickselect(a, lower, upper, k):
    if lower == upper:
        return a[lower]
    else:
        pivot_index = partition_Hoare_wrapper(a, lower, upper)
        if pivot_index == k - 1:
            return a[pivot_index]
        elif pivot_index < k - 1:
            return quickselect(a, pivot_index + 1, upper, k)    
        else:
            return quickselect(a, lower, pivot_index - 1, k)

Архив с файлом можно взять здесь.

Оценка времени выполнения алгоритма зависит от положения опорного элемента после выполнения декомпозиции. Если он всегда находится в середине списка, время выполнения характеризуется функцией

            1,           если n ≤ 1,
    T(n) =  
            T(n/2) + c_n, если n > 1,

поскольку алгоритму требуется решить подзадачу примерно в половину размера исходной задачи, так как основанные на разбиении методы работают за линейное время. Это лучший вариант развития событий, когда T(n) ∈ Θ(n). Однако если опорный элемент всегда оказывается в крайних позициях списка, время выполнения может быть оценено функцией

            1,             если n ≤ 1,
    T(n) = 
            T(n - 1) + c_n, если n > 1,

которая является квадратичной, то есть T(n) ∈ Θ(n²). Эта ситуация соответствует худшему варианту развития событий в алгоритме.

На следующем шаге мы рассмотрим двоичный поиск корня функции.

Предыдущий шаг Содержание Следующий шаг