На этом шаге мы рассмотрим особенности рекурсивной реализации этого алгоритма.

Алгоритм быстрой сортировки quicksort - ещё один метод, разработанный Чарльзом Хоаром. В нём применён подход "разделяй и властвуй", и он получил свое название из-за своей поразительной эффективности. В отличие от алгоритма сортировки слиянием время его выполнения в худшем случае - Ο(n²). Однако в лучших и средних случаях он выполняется за время Θ(n log n) и может быть практически в несколько раз быстрее алгоритма сортировки слиянием.

Чтобы понять разницу между двумя методами, отметим, что декомпозиция в сортировке слиянием проста. В частности, входной список можно разделить пополам, используя просто соответствующие индексные диапазоны (0:n//2 и n//2:n). Однако объединение результатов подзадач требует решения еще одной задачи - слияния, которая не очень проста. Напротив, в алгоритме quicksort декомпозиция сложна, однако этап объединения не только тривиален, но в некоторых реализациях даже не всегда нужен.

А именно вместо простого деления списка пополам декомпозиция quicksort использует схему разделения, подобную схеме из 88 шага. Рисунок 1 иллюстрирует такой тип декомпозиции, когда подсписки внутри исходного списка разделены опорным элементом: элементы правого списка не больше опорного, а левого - больше опорного.

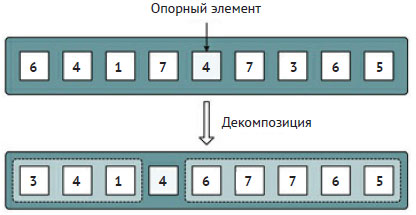
Рис.1. Декомпозиция алгоритма quicksort

Примерная рекурсивная схема при такой декомпозиции могла бы быть такой:

Из схемы видно, что сортировка исходного списка требует сначала решения двух подзадач посредством рекурсивных вызовов и затем объединения отсортированных подсписков при обработке опорного элемента между ними. Таким образом, после рекурсивного решения подзадач объединение их результатов становится простым. Наконец, важная деталь этой декомпозиции заключается в том, что опорный элемент удаляется из списка не превосходящих его элементов. Это - гарантия того, что размер подзадачи действительно меньше размера исходной задачи.

В примере 6.4 приводится более медленный вариант метода, основанный на простых схемах разделения из 89 шага.

Сначала он проверяет, соответствует ли вход начальному условию (которое является тем же, что в методе сортировки слиянием). В рекурсивном условии общая стратегия состоит в том, что в качестве опорного элемента берётся первый элемент списка. При таком выборе возможен наихудший случай, когда входной список уже отсортирован. Кроме того, этот алгоритм может оказаться плохим ещё и тогда, когда вход почти отсортирован. Поскольку такие ситуации возникают на практике довольно часто, функция использует в качестве опорного средний элемент входного списка. После этого метод, согласно декомпозиции, получает два подсписка (удаляя опорный элемент из содержащего его подсписка) и наконец объединяет результаты подзадач, вставляя опорный элемент между ними.

Пример 6.4. Вариант алгоритма quicksort

1
2
3
4
5
6
7
8
9
10
11

def quicksort_variant(a):
    n = len(a)
    if n <= 1:
        return a
    else:
        pivot = a[n // 2]
        v1 = get_smaller_than_or_equal_to(a, pivot)    
        v1.remove(pivot)
        v2 = get_greater_than(a, pivot)
        return (quicksort_variant(v1) + [pivot]    
                + quicksort_variant(v2))

Архив с файлом можно взять здесь.

Метод сортировки слиянием в примере 6.2 и функция quicksort() в примере 6.4 не меняют входной список и возвращают свои результаты в новом списке, что требует вдвое больше памяти. Такие типы алгоритмов называются алгоритмами "внешней" сортировки. Вместо этого можно реализовать варианты, которые изменяют входной список и не требуют дополнительной памяти для всего списка длины n. Такие алгоритмы называются алгоритмами "внутренней" сортировки. В примере 6.5 приводится алгоритм quicksort() внутренней сортировки, использующий нижний и верхний пределы для указания границ подсписка внутри исходного списка. Код включает рекурсивную версию метода разбиения Хоара из примера 5.13 (конечно, более эффективная итерационная версия тоже допустима), выполняющего декомпозицию задачи.

Пример 6.5. Алгоритм внутренней сортировки quicksort

1
2
3
4
5
6

def quick_sort_inplace(a, lower, upper):
    if lower < upper:
        pivot_index = partition_Hoare_wrapper(a, lower, upper)    

        quick_sort_inplace(a, lower, pivot_index - 1)
        quick_sort_inplace(a, pivot_index + 1, upper)

Архив с файлом можно взять здесь.

Оценка времени выполнения алгоритма подобна таковой для алгоритма quickselect. Основное различие - в том, что вместо решения одной подзадачи quicksort решает две, вызывая себя дважды. Наилучший случай - когда опорный элемент всегда находится в середине списка. В этом случае время выполнения характеризуется функцией

            1,           если n ≤ 1,
    T(n) =  
            T(n/2) + cⁿ, если n > 1,

где T(n) ∈ Θ(n logn). Наоборот, худший случай - когда опорный элемент всегда располагается в крайнем положении списка. В этом случае время выполнения определяется функцией

            1,             если n ≤ 1,
    T(n) = 
            T(n - 1) + cⁿ, если n > 1,

которая имеет квадратичный порядок роста (T(n) ∈ Θ(n²)).

На следующем шаге мы рассмотрим мажоритарный элемент списка.

Предыдущий шаг Содержание Следующий шаг