На этом шаге мы рассмотрим рекурсивную реализацию такого обхода.

    Рассмотрим задачу печати узлов двоичного дерева поиска (см. 85 шаг "Двоичные деревья поиска") в порядке следования его ключей. Рекурсивный алгоритм решения задачи можно разработать следующим образом. Понятно, если дерево пусто, то алгоритм не выполняет никаких действий. Это - начальное условие. Для вывода рекурсивного условия рассмотрим схему на рисунке 1, где корень дерева отбрасывается, а дерево разбивается на левое поддерево и правое поддерево.

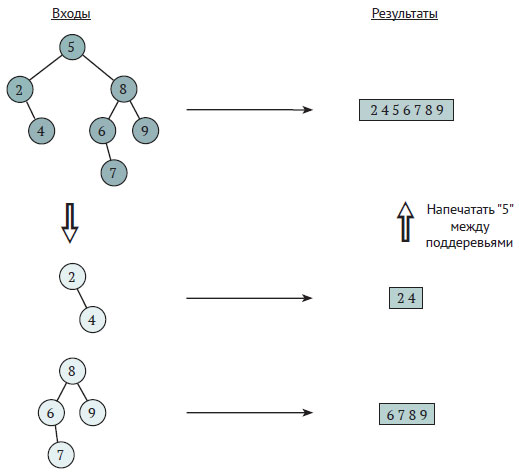
Рис.1. Пример декомпозиции задачи внутреннего обхода дерева

    В первую очередь мы уверены, что любой ключ левого поддерева меньше ключа его корня. Кроме того, согласно основному свойству двоичных деревьев поиска левое поддерево - это тоже двоичное дерево поиска. Поэтому согласно принципу индукции можно считать, что рекурсивный вызов для левого поддерева, как и рекурсивный вызов для правого поддерева, напечатает свои ключи в нужном порядке. Отсюда понятно, что метод просто должен получить результаты обеих подзадач, а между ними напечатать ключ корневого узла.

    Процедура внутреннего обхода дерева приведена в примере 7.4, где предполагается, что каждый узел исходного двоичного дерева поиска - это список из четырех элементов (см. 85 шаг "Двоичные деревья поиска").

def inorder_traversal(T):
    if T != []:
        inorder_traversal(T[2])  # обработать левое поддерево
        print(T[0], ': ', T[1], sep='')  # печать ключа и значения    
        inorder_traversal(T[3])  # обработать правое поддерево

    Например, применительно к дереву дней рождения из (5.1) этот код напечатает элементы дерева в алфавитном порядке имён (ключей) людей (рисунок 2).

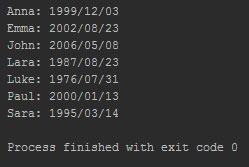
Рис.2. Результат работы приложения

    Таким образом, мы говорим, что метод выполняет внутренний (inorder) обход двоичного дерева поиска.

    На следующем шаге мы рассмотрим прямой и обратный обходы.

Предыдущий шаг Содержание Следующий шаг