На этом шаге мы рассмотрим рекурсивное решение этой задачи.
Цель следующей задачи - посчитать количество возможных способов подняться по лестнице из n ступенек с шагом в одну или две ступеньки. На рисунке 1 показан один из способов подъёма по лестнице из семи ступенек.
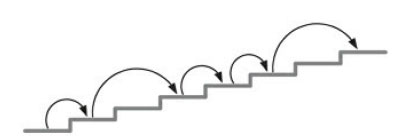
Рис.1. Один из способов подняться по лестнице с шагом в 1 или 2 ступеньки
Понятно, что размер задачи - n. Рассмотрим несколько начальных условий. Если n = 1, то существует только один способ подняться по лестнице. Если n = 2, то можно сделать либо два шага, либо один (через ступеньку). Кроме того, если представлять способ подъёма списком, то можно также считать, что при n = 0 результатом будет пустой список.
В исходной задаче (рисунок 2(а)) темная стрелка представляет общее количество способов f(n) подъёма по лестнице из n ступенек.
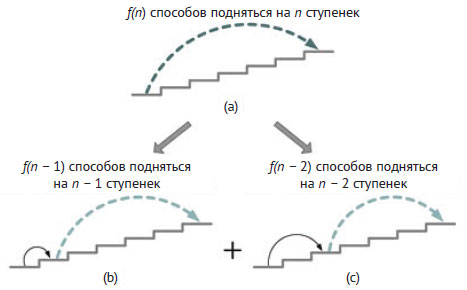
Рис.2. Декомпозиция задачи подсчёта всех способов подняться по лестнице с шагом в 1 или 2 ступеньки
А сами способы подъёма можно разделить на две группы. Одна из них включает последовательность дальнейших шагов после одиночного шага. После одиночного шага будет ещё f(n - 1) способов добраться до вершины лестницы, делая одиночные или двойные шаги (рисунок 2(b)). Поэтому жирная стрелка представляет подзадачу размера n - 1. Во второй группе - дальнейшая последовательность шагов после двойного шага. В этом случае (рисунок 2(c)) количество способов подняться по лестнице будет f(n - 2), где жирная стрелка указывает на подзадачу размера n - 2. Наконец, поскольку обе группы последовательностей представляют общее количество способов подняться по лестнице, решение - f(n - 1) + f(n - 2). Вместе с начальными условиями функция может быть определена следующим образом:
1, если n = 1,
f(n, k) = 2, если n = 2,
f (n - 1) + f (n - 2), если n ≥ 3
На следующем шаге мы рассмотрим путь по Манхэттену.
