На этом шаге мы рассмотрим особенности рекурсивного вычисления сочетаний.

Сочетание из n различных элементов по k без повторений - это просто подмножество из k элементов исходного множества. Сочетания подобны размещениям, только порядок следования элементов здесь не имеет значения. Поэтому сочетание соответствует (под)множеству, а не последовательности. Например, подмножество {а₁, а₂, а₃} - это сочетание элементов на множестве {а₁, а₂, ..., а₁₀}, причём {а₁, а₂, а₃} и {а₃, а₁, а₂} не различаются. На этом шаге мы займёмся подсчётом всех сочетаний из n различных элементов по k элементов без повторений.

Размер этой задачи зависит и от k, и от n (где k < n). Как мы вскоре увидим, для разработки рекурсивного решения их необходимо уменьшать вместе. Но мы начнём с определения начальных условий. Тривиальное выполняется при k = n, когда существует лишь одно правильное сочетание - это всё множество из n элементов. Другое простое условие выполняется при k = 1, когда результат, очевидно, равен n. Кроме того, при k = 0 можно считать, что есть только одна правильная комбинация - пустое множество. Как и в предыдущих шагах, если у нас есть начальное условие для k = 0, то необходимость в начальном условии для k = 1 отпадает.

Для вывода рекурсивного условия разобьём все сочетания на два множества. Рассмотрим исходное множество из n элементов {а₁, а₂, ..., а_n} и отдельный его элемент, скажем, а₁. Обратите внимание, что существует два типа сочетаний:

(а) содержащие а₁ и
(b) не содержащие а₁.

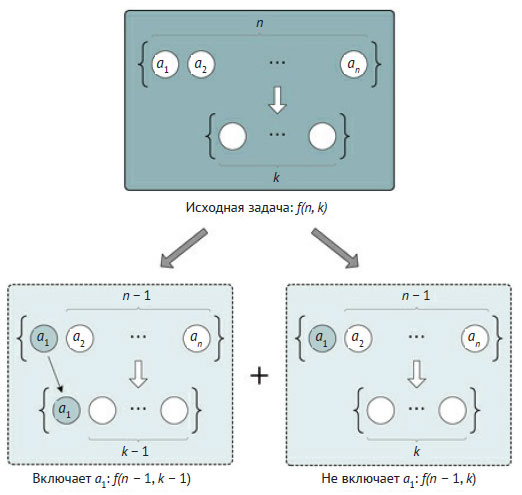
Таким образом, исходную задачу f(n, к) можно разбить на две в зависимости от типа сочетания, как показано на рисунке 1.

Рис.1. Декомпозиция задачи подсчёта сочетаний из n элементов по k

Если сочетания содержат а₁, то оставшиеся k - 1 элементов - это сочетания из n - 1 элементов подмножества {а₂, ..., а_n} по k - 1 элементов. А этот набор сочетаний определяется функцией f(n - 1, k - 1). Если же а₁ не содержится в сочетаниях, то это - сочетания из того же подмножества {а₂, ..., а_n} по k элементов, а количество таких сочетаний - f(n - 1, k). Таким образом, результатом будет сумма обоих типов сочетаний, а рекурсивная формула - f(n, k) = f(n - 1, k - 1) + f(n - 1, k). В итоге вместе с начальными условиями функция определяется как

              1,                             если k = 0 или k = n,
    f(n, k) =                                            
              f(n - 1, k - 1) + f(n - 1, k), в противном случае,

и определяет биномиальный коэффициент (см. (3.2)).

На следующем шаге мы рассмотрим подъём по лестнице.

Предыдущий шаг Содержание Следующий шаг