На этом шаге мы рассмотрим особенности реализации рекурсивного вычисления этого пути.
Во многих городах улицы и авеню перпендикулярны друг другу. Предположим, что они образуют прямоугольную систему координат, как на рисунке 1.
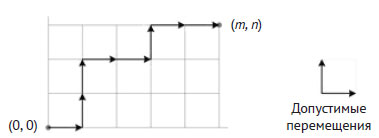
Рис.1. Задача о пути по Манхэттену
Цель задачи - определить количество путей, ведущих к пересечению авеню m ≥ 0 с улицей n ≥ 0 (где m и n - целые числа), начиная с авеню 0 и улицы 0. Чтобы это сделать, предположим, что на каждом шаге разрешается идти только к улице или авеню с большим номером, то есть вверх или вправо.
Можно считать, что размер задачи - min(m, n). В этом случае простейшее начальное условие выполняется, когда один из параметров равен 0, поскольку в этом случае к точке (m, n) ведёт только один правильный путь по прямой. Кроме того, если оба параметра равны 0, такой путь можно считать "пустым".
Задачу можно разбить на две отдельные подзадачи, как показано на рисунке 2.
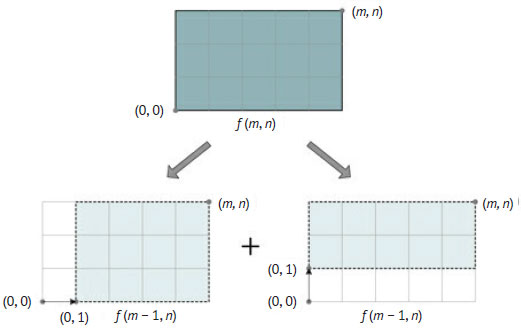
Рис.2. Декомпозиция задачи о пути по Манхэттену
Пусть f(m, n) - общее количество путей от (0, 0) к (m, n). Обратите внимание, что можно разделить пути на два несвязных множества в зависимости от выбора первого шага. Если мы пошли вправо к точке (1, 0), то от неё до (m, n) будет f(m - 1, n) путей. И наоборот, если мы пошли вверх к точке (0, 1), то от неё до (m, n) будет f(m, n - 1) путей. Сумма этих количеств даст рекурсивное решение. Функция выглядит следующим образом:
1, если n = 0 или m = 0,
f(n, k) =
f (m - 1, n) + f (m, n - 1), в противном случае.
Наконец, путь к (m, n) - это последовательность из m + n шагов, где m - количество шагов вправо, а n - количество шагов вверх. Иными словами, весь путь можно представить двоичной последовательностью длины m + n. Следовательно, его можно задать последовательностью направлений движения - вправо (это сочетание из n + m элементов по m) или, аналогично, прямо (это сочетание из n + m элементов по n). Таким образом, функция - это биномиальный коэффициент:
n m f(m, n) = C = C = (m + n)! / (m! * n!) m+n m+n
В итоге можно считать, что формула определяет количество сочетаний из m + n элементов по m или по n элементов, где количество шагов вправо m, как и количество шагов вверх n, неизменно.
На следующем шаге мы рассмотрим триангуляцию выпуклого многоугольника.
