На этом шаге мы рассмотрим общий рекурсивный принцип решения этой задачи.
Триангуляция многоугольника - это множество непересекающихся треугольников, которые покрывают (без перекрытий) всю область многоугольника и вершины которых являются вершинами многоугольника. На рисунке 1 показаны две триангуляции выпуклого 7-угольника (выпуклый многоугольник - это многоугольник, в котором любой отрезок, соединяющий любые две его внутренние точки, лежит внутри многоугольника).
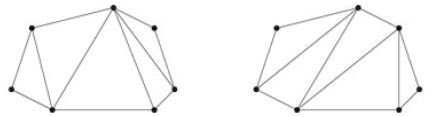
Рис.1. Две возможные триангуляции одного выпуклого 7-угольника
Следующая задача состоит в определении функции, вычисляющей все возможные различные способы разбиения выпуклого n-угольника на треугольники.
Размер задачи - n. Тривиальное начальное условие выполняется при n = 3, когда результат, очевидно, равен 1. Кроме того, подобно предыдущим задачам, если n = 2, то результат тоже равен 1 (что будет уточнено ниже).
Рекурсивное условие здесь сложнее, чем в предыдущих примерах, так как решение потребует рассмотрения нескольких подзадач меньшего размера. Для понимания декомпозиции воспользуемся конкретным примером. Рассмотрим, например, нижнюю сторону 8-угольника на рисунке 2.

Рис.2. Шесть (n - 2) треугольников на базе нижней стороны восьмиугольника (n = 8)
Естественно, что она должна принадлежать одному из треугольников триангуляции, но таких различных треугольников, включающих эту сторону, - 6 (n - 2) по числу вершин многоугольника, не принадлежащих его нижней стороне. Поэтому триангуляции могут быть разбиты на 6 независимых множеств, отвечающих конкретному треугольнику на базе нижней стороны. Другими словами, затененный треугольник определяет соответствующее ему множество триангуляций, а общее количество триангуляций будет суммой триангуляций в каждом из шести множеств.
Выбрав один из затенённых треугольников, по обе его стороны мы получим два выпуклых многоугольника (один из которых может быть пустым), которые также должны быть разбиты на треугольники. Отметим, что оба многоугольника примыкают к сторонам затенённого треугольника. Согласно принципу умножения, общее количество триангуляций, связанных с выбранным затенённым треугольником, будет равно произведению числа триангуляций каждого из смежных многоугольников, как показано на рисунке 3.
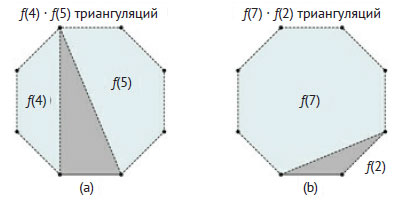
Рис.3. Декомпозиция задачи триангуляции выпуклого многоугольника для конкретного треугольника
Пусть f(n) - целевая функция задачи, тогда на рисунке 3(a) слева от затенённого треугольника - подзадача размера 4, а справа - подзадача размера 5. Количество триангуляций, связанных с затенённым треугольником, будет f(4) * f(5). В случае (b) одна из подзадач имеет размер 7, а вторая - размер 2, поэтому мы имеем f(7) * f(2) триангуляций, связанных с затенённым треугольником. Несмотря на то что один из многоугольников (связанный с f(2)) пуст, количество возможных триангуляций, связанных с затенённым треугольником, даст f(7), что подтверждает использование в качестве начального условия f(2) = 1.
В конце концов, нужно сложить все триангуляции, связанные с шестью затененными треугольниками. В приведённом примере, как показано на рисунке 4, мы получим:
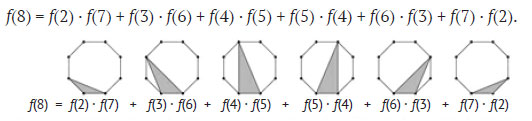
Рис.4. Общее количество триангуляций в восьмиугольнике
В общем виде рекурсивную функцию можно определить как
1, если n = 2,
f(n) =
n-1
∑ f(i) * f(n + 1 - i), если n > 2 .
i=2
Отметим, что дополнительное начальное условие для n = 3 необязательно.
Наконец, f(n) имеет отношение к часто встречающимся в комбинаторике числам Каталана и может быть определена как
1, если n = 0,
C(n) = (8.1)
n-1
∑ С(i) * С(n - 1 - i), если n > 0 .
i=0
В частности, f(n) = C(n - 2)
На следующем шаге мы рассмотрим пирамиды из кругов.
