На этом шаге мы рассмотрим рекрсивную реализацию этой задачи.
В следующей задаче нужно определить количество возможных способов укладки кругов рядами внутри пирамиды. Начав с непрерывного ряда кругов в основании, нужно укладывать на него круги согласно следующим правилам:
- 1) все круги в ряду должны примыкать друг к другу, то есть между ними не должно быть промежутков;
- 2) каждый круг не из нижнего ряда должен лежать на двух кругах рядом ниже, образуя равносторонний треугольник ("пирамиду").
На рисунке 1 приведены примеры правильных и неправильных укладок кругов. Задача состоит в том, чтобы определить функцию, которая подсчитывает количество правильных укладок кругов, начиная с n кругов нижнего ряда.
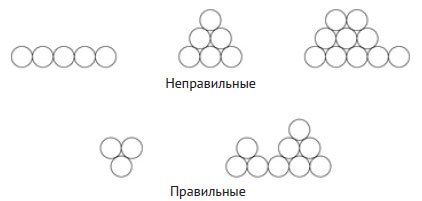
Рис.1. Правильные и неправильные пирамиды из кругов
Размер задачи - n. Тривиальное начальное условие выполняется при n = 1, когда результат, очевидно, равен 1. Для вывода рекурсивного условия будем делить возможные пирамидальные конфигурации на несколько несвязных групп по количеству кругов непосредственно над нижним рядом. Рисунок 2 иллюстрирует эту идею для n = 4.

Рис.2. Пирамиды, сгруппированные по количеству кругов непосредственно над нижним рядом из n = 4 кругов
Ключ к решению - в том, что меньшие пирамиды (подзадачи) с одинаковым количеством кругов в нижнем ряду можно разместить несколькими способами над нижним рядом кругов исходной задачи (см. рисунок 3).
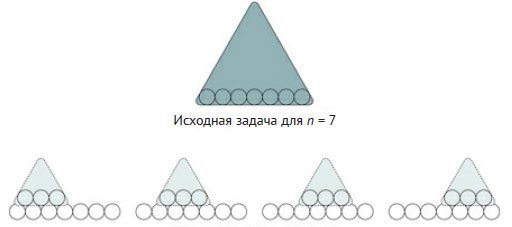
Рис.3. Декомпозиция задачи о пирамиде из кругов на подзадачи конечного размера
В частности, для начального входного параметра n существует n - i способов размещения подобной пирамиды размера i. На рисунке i = 3 и n = 7, тогда существует n - i = 4 способа разместить подобные исходной пирамиды размера 3 над нижним рядом из n = 7 кругов.
В итоге, поскольку размер меньших подзадач варьируется от 1 до n - 1, функция должна сложить все возможные конфигурации кругов. Кроме того, поскольку сам полный нижний ряд кругов (без кругов над ним) считается правильной укладкой, к функции следует добавить ещё 1. Ниже приведена функция, решающая задачу:
1, если n = 1,
f(n) = (8.2)
n-1
1 + ∑ (n - i) * f(i), если n > 1 .
i=1
Таким образом, результат представляет собой функцию Фибоначчи. В частности, можно доказать, что f(n) = F(2n - 1), где F - функция Фибоначчи.
На следующем шаге мы приведем решения нескольких задач.
