На этом шаге мы рассмотрим несколько заданий и приведем их решения.

    Приведем несколько примеров решения задач.

    Задание 1. У нас есть n одинаковых костей для игры в "домино" размера 1*2 (или 2*1 при повороте на 90°). Выведите рекурсивную функцию, определяющую количество способов выложить из костей (без наложений и дыр) прямоугольник размером 2*n. На рисунке 1 приведён конкретный пример для n = 10.

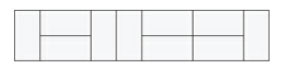
Рис.1. Выкладывание прямоугольника размером 2*10 из костей домино размером 1*2 или 2*1

Раскрыть/скрыть решение и комментарии.

def f(n):
    if n == 1:
        return 1
    elif n == 2:
        return 2
    else:
        return f(n - 1) + f(n - 2)    

    Задание 2. Баскетбольная команда может набирать очки тремя различными способами: штрафной бросок - одно очко, бросок с игры (в пределах трёхочковой зоны) - два очка и бросок из-за трёхочковой зоны - три очка. Найдите функцию, определяющую количество вариантов набора баскетбольной командой n очков. Например, существует 4 варианта набрать 3 очка: 1 + 1 + 1, 1 + 2, 2 + 1 и 3. Как видим, последовательность получения очков имеет значение.

Раскрыть/скрыть решение и комментарии.

def f(n):
    if n == 1:
        return 1
    elif n == 2:
        return 2
    elif n == 3:
        return 4
    else:
        return f(n - 1) + f(n - 2) + f(n - 3)    

    Задание 3. Реализуйте функцию вычисления чисел Каталана C(n) в (8.1).

Раскрыть/скрыть решение и комментарии.

def f(n):
    if n == 0:
        return 1
    else:
        s = 0
        for i in range(n):    
            s += f(i) * f(n - 1 - i)    
        return s

    Со следующего шага мы начнем рассматривать множественную рекурсию.

Предыдущий шаг Содержание Следующий шаг