На этом шаге мы рассмотрим особенности решения этой задачи.

    Следующая задача является разновидностью классической задачи "Ханойская башня" (см. 112 шаг) и известна как "циклические" ханойские башни. Несмотря на то что вводимое в ней ограничение усложняет задачу, принцип её решения и само решение (то есть перемещение отдельных дисков или стопок из нескольких дисков) аналогичны. Таким образом, она представляет собой превосходное дополнение к оригинальной задаче, которое поможет лучше понять её решение. Кроме того, она подтверждает важность рекурсии для решения задач вообще, так как (насколько известно) единственный из итерационных алгоритмов решения этой задачи просто моделирует её рекурсивное решение, используя стек.

    Правила циклических ханойских башен идентичны правилам оригинальной задачи с той лишь разницей, что перемещать отдельные диски можно только циклически (по кругу). Например, если A, B и C обозначают три стержня, то диск можно перемещать только с A на B, с B на C или с C на A. Задача становится наглядней, если стержни расположить в виде треугольника и разрешить перемещения дисков только по кругу в определенном направлении, скажем по часовой стрелке, как на рисунке 1.

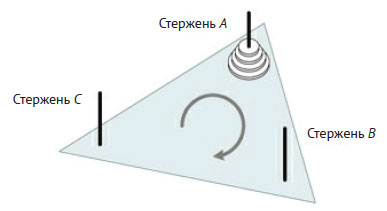
Рис.1. Циклические ханойские башни

    Задача заключается в том, чтобы переместить всю стопку из n дисков с исходного (начального) стержня, скажем A, на другой заданный (конечный) стержень, используя третий вспомогательный (промежуточный) стержень. Обратите внимание, что условие задачи не оговаривает, какой именно стержень, B или C, должен быть конечным. Несмотря на то что мы условились перемещать диски по часовой стрелке, важно понимать, что на самом деле можно написать разные процедуры для перемещения всей стопки из n дисков как по часовой стрелке, так и против часовой стрелки. Иными словами, задача о циклических ханойских башнях состоит из двух разных задач: перемещение n дисков по часовой стрелке или против часовой стрелки, но при этом каждый отдельный диск должен перемещаться по кругу только в одном направлении. Обе задачи изображены на рисунке 2, где O, D и A обозначают соответственно начальный, конечный и вспомогательный стержни.

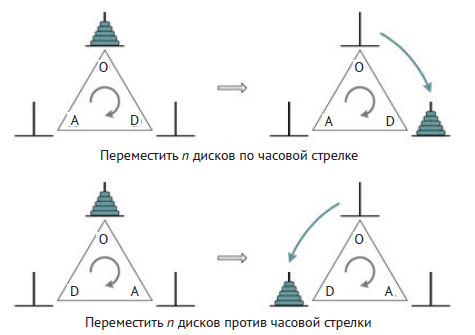
Рис.2. Две разновидности задачи о циклических ханойских башнях

    Заметьте, что конечный и вспомогательный стержни меняются местами в зависимости от варианта задачи.

    Понятно, что размер обеих задач - n. Первое начальное условие имеет место при n = 1. Это тривиальное решение предполагает одно перемещение единственного диска по часовой стрелке или два перемещения того же диска против часовой стрелки. Второе начальное условие, подобно функции towers_of_Hanoi_alt() в примере 7.3, предупреждает какие-либо действия при n = 0.

    Для вывода рекурсивных условий можно применить декомпозицию задачи с уменьшением её размера на 1, что приведёт к трём действиям, лежащим в основе рекурсивных методов её решения (см. рисунок 3).

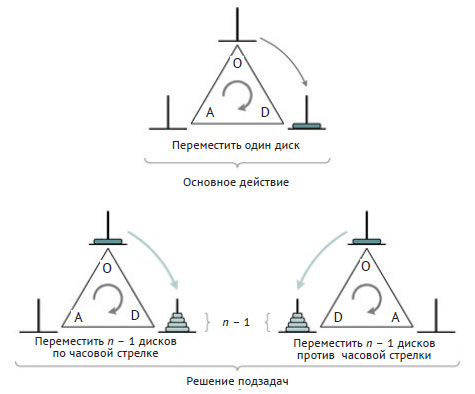
Рис.3. Три действия рекурсивных методов, решающих задачу о циклических ханойских башнях

    Во-первых, согласно правилам задачи, отдельный диск можно переместить по часовой стрелке. Во-вторых, согласно индукции, стопку из n - 1 дисков можно переместить либо по часовой стрелке, либо против неё.

    На рисунке 3 показаны шаги решения задачи по перемещению стопки из n дисков по часовой стрелке с начального стержня на конечный. Сначала нужно переместить n - 1 дисков на вспомогательный стержень, так как иначе невозможно переместить наибольший диск. Добиться этого можно перемещением стопки из n - 1 дисков против часовой стрелки с начального стержня на вспомогательный при посредстве конечного стержня (шаг 1). На следующем, основном шаге 2 на конечный стержень переносится наибольший диск. А затем n - 1 дисков переносятся со вспомогательного стержня на конечный, что также осуществляется их перемещением против часовой стрелки (шаг 3).

    Процедура clockwise() в примере 9.6 реализует этот метод. Ход рассуждений при решении данной задачи очень похож на тот, что применялся при решении оригинальной задачи о ханойских башнях. Таким образом, алгоритм почти совпадает с кодом примера 7.3, за исключением того, что рекурсивные вызовы обращаются ко второму методу. Заметим, что при программировании алгоритма в целом мы предполагаем, что перемещения против часовой стрелки работают правильно, даже если мы не написали для них ни одной строки кода.

def clockwise(n, o, d, a):
    if n > 0:
        counterclockwise(n - 1, o, a, d)
        print('Переместить диск', n, 'со стержня', o, 'на стержень', d)    
        counterclockwise(n - 1, a, d, o)


def counterclockwise(n, o, d, a):
    if n > 0:
        counterclockwise(n - 1, o, d, a)
        print('Переместить диск', n, 'со стержня', o, 'на стержень', d)
        clockwise(n - 1, d, o, a)
        print('Переместить диск', n, 'со стержня', а, 'на стержень', d)
        counterclockwise(n - 1, o, d, a)

    Наконец, на рисунке 4 показаны действия по перемещению стопки из n дисков против часовой стрелки, осуществляемые процедурой counterclockwise() из примера 9.6.

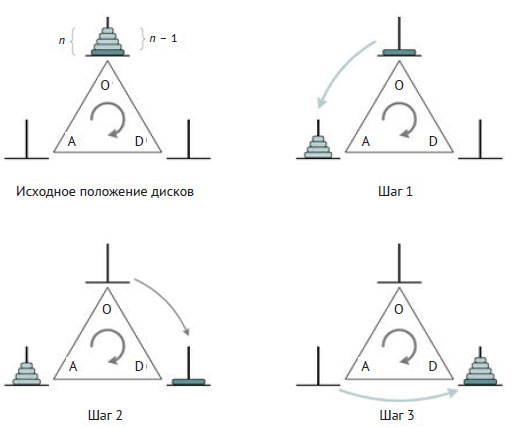
Рис.4. Действия по перемещению n дисков против часовой стрелки

    В этом случае требуется больше работы, так как для воспроизведения единственного перемещения наибольшего диска по часовой стрелке здесь необходимо два его перемещения против часовой стрелки. Первый шаг с рекурсивным вызовом - это n - 1 перемещений против часовой стрелки, обеспечивающих выполнение основного действия по переносу наибольшего диска на вспомогательный стержень (шаг 2). На шаге 3 стопка из n - 1 дисков возвращается по часовой стрелке на начальный стержень (вызывая уже реализованный метод clockwise()), чтобы тем самым подготовить второе основное действие на шаге 4 - перемещение наибольшего диска на конечный стержень. После этого выполняется заключительное действие - перемещение против часовой стрелки стопки из n - 1 дисков на конечный стержень.

    Со следующего шага мы начнем рассматривать грамматики и синтаксический анализатор на основе рекурсивного спуска.

Предыдущий шаг Содержание Следующий шаг