На этом шаге мы сравним хвостовую рекурсию и итерацию.

    Итерационные программы могут быть преобразованы в рекурсивные, и наоборот. Более того, связь между итерацией и хвостовой рекурсией особенно очевидна. Этот раздел исследует эту связь и объясняет, почему хвостовой рекурсии обычно предпочитают итерацию.

    Вообще говоря, любые рекурсивные алгоритмы могут быть преобразованы в равносильные итерационные версии с использованием стековой структуры данных, исполняющей роль программного стека. Однако для хвостовых рекурсивных методов это преобразование гораздо проще, поскольку оно не нуждается в стеке. Всё дело в том, что хвостовые рекурсивные алгоритмы, в сущности, не обязаны хранить информацию в программном стеке, так как они не нуждаются в стеке при возврате из подпрограммы (метода).

    Рассмотрим ещё раз линейно-рекурсивную функцию sum_first_ naturals() из примера 1.1. Она требует сохранения в программном стеке значений аргументов (см. рисунок 3 159 шага), которые для получения конечного результата используются и обрабатываются затем вместе с результатами рекурсивных вызовов. Например, sum_first_naturals(4) выталкивает из стека аргумент 4 и добавляет его к результату sum_first_naturals(4), открывая тем самым аргумент sum_first_naturals(3). Напротив, функция gcdl() в примере 5.18 получает свой конечный результат после обработки начального условия, так как здесь имеет место хвостовая рекурсия. В частности, на рисунке 1 приводится программный стек при вызове gcd1(20, 24) на момент проверки начального условия.

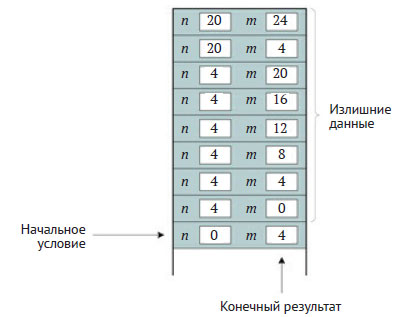
Рис.1. Состояние программного стека при вызове gcd1(20,24) на момент проверки начального условия

    Этот рисунок похож на дерево активации на рисунок 1 161 шага или на (5.6), где результат метода (4) достигается в начальном условии и без изменений возвращается каждым рекурсивным вызовом. Это значит, что все хранящиеся в программном стеке данные никогда не используются и потому не нужны. Действительно, получив результат в начальном условии, программа просто передаёт его без изменений самому первому рекурсивному вызову, последовательно удаляя каждый стековый кадр по завершении каждого рекурсивного вызова.

    Этот пример показывает, что можно создать равносильный итерационный алгоритм вычисления наибольшего общего делителя без использования стека. В частности, функция gcdl() нуждается в единственном цикле, в котором нужно изменять значения параметров n и m, когда она вызывает саму себя. Другими словами, цикл должен смоделировать изменение параметров при переходе от очередного стекового кадра к следующему, как на рисунке 1. Следовательно, на каждом шаге цикла, в сущности, должны выполняться те же самые обновления параметров, что выполняются при вызове хвостовой рекурсивной функции (отметим, что рекурсивное условие хвостового рекурсивного метода задаёт лишь изменение параметров от одного вызова до следующего). Наконец, условие выхода из цикла должно быть таким же, как для начального условия.

    В примере 11.1 приведён этот альтернативный итерационный вариант. Начальное условие в gcdl() достигается при m = 0.

def gcd1_iterative(m, n):  
    while m > 0:
        if m > n:
            aux = n
            n = m
            m = aux
        else:
            n = n - m

    return n

    Таким образом, рекурсивные условия выполняются при m > 0. Поэтому мы можем использовать цикл, который выполняется, пока m > 0, и который моделирует все выполняемые gcdl() рекурсивные вызовы вплоть до достижения начального условия. Рекурсивных условий здесь два. Если m > n, то рекурсивный вызов просто меняет параметры местами (строки 4-6) с использованием вспомогательной переменной. При выполнении второго рекурсивного условия m < n значение n просто меняется на n - m (строка 8). Наконец, когда m = 0, метод просто возвращает значение n, согласно начальному условию gcdl().

    Итерационные аналоги хвостовых рекурсивных алгоритмов обладают двумя преимуществами. С одной стороны, они более эффективны, так как не нуждаются в программном стеке и могут вернуть результат, как только он вычислен. Отметим, что итерационный алгоритм возвращает результат только один раз, тогда как хвостовой рекурсивный возвращает одно и то же значение многократно. С другой стороны, они не приводят к переполнению стека даже для больших значений входных параметров. Если количество рекурсивных вызовов ограничено, то количество итераций цикла (который, в сущности, выполняет те же вычисления, что и рекурсивные вызовы) не ограничено. Для большинства приложений потеря эффективности от применения хвостовых рекурсивных методов не имеет значения. Однако ограничение на количество рекурсивных вызовов - важный фактор масштабируемости (универсальности) рекурсивных алгоритмов, представляющий гораздо более серьезную проблему.

    Однако если рекурсивный алгоритм делит размер задачи на два (или на другую константу), ограничение на количество рекурсивных вызовов обычно не представляет проблемы. Для таких алгоритмов высота дерева рекурсии является логарифмической функцией размера задачи. Таким образом, для решения задачи вряд ли потребуется большое количество вложенных рекурсивных вызовов (например, 1000). Если же эффективность алгоритма тоже не важна, то хвостовой рекурсивный алгоритм - вполне приемлемое решение. Рассмотрим, например, хвостовую рекурсивную функцию bisection() из примера 5.15, относящуюся к методу деления пополам. Если она используется для вычисления квадратного корня, то количество выполняемых ею рекурсивных вызовов относительно мало. Например, вызов bisection(0, 4, f, 10**(-10)) требует всего 36 рекурсивных вызовов, чтобы приблизиться к значению √4 = 2 с точностью до девяти десятичных цифр после запятой. Более того, при таком небольшом количестве рекурсивных вызовов разница во времени выполнения, по сравнению с аналогичным итерационным алгоритмом из примера 11.2, будет совсем незначительной.

    Для моделирования рекурсивных вызовов метод также использует цикл while, в условии которого - инвертированное начальное условие рекурсивной функции. Условный оператор if различает два сценария, соответствующих двум рекурсивным условиям. В обоих случаях обновляется только один параметр. Наконец, в каждой итерации значение переменной z обновляется для сохранения окончательного результата. Поскольку оба алгоритма практически одинаковы, предпочтение можно отдать тому, который проще читается. В данном случае оба алгоритма просты в понимании той задачи, которую они решают. Однако хвостовые рекурсивные методы больше опираются на декомпозицию задачи.

def bisection_iterative(a, b, f, epsilon):
    z = (a + b) / 2

    while f(z) != 0 and b - a > 2 * epsilon:
        if (f(a) > 0 and f(z) < 0) or (f(a) < 0 and f(z) > 0):  
            b = z
        else:
            a = z

        z = (a + b) / 2

    return z

    Наконец, для повышения эффективности многие современные компиляторы в состоянии обнаружить хвостовые рекурсивные методы и автоматически преобразовать их в итерационные версии. К сожалению, в языке Python нет такой возможности, которую часто называют "устранением хвостовой рекурсии" (tail-recursion elimination). Один из аргументов автора языка Python Гуидо ван Россума состоит в том, что это усложняет отладку. Поэтому он рекомендует использовать вместо хвостовой рекурсии итерацию. По нашему мнению, если эффективность и ограничение на размер программного стека актуальны, то, очевидно, нужно пользоваться итерационными методами вместо хвостовых рекурсивных. Если же они не актуальны, то программистам следует предпочесть реализацию, которая больше соответствует их пониманию решения задачи. Короче говоря, предпочтение отдаётся той версии, которую проще понять и легче сопровождать.

    На следующем шаге мы рассмотрим итерационный подход к хвостовой рекурсии.

Предыдущий шаг Содержание Следующий шаг