На этом шаге мы рассмотрим реализацию этой задачи.

Цель этой задачи - в том, чтобы для заданного множества S из n положительных целых чисел и заданного целого числа х найти в S такое подмножество, сумма элементов которого равна х. Формально, если s_i - i-е целое число множества S, то задача состоит в том, чтобы найти такое подмножество T ⊆ S, что:

   ∑ s_i = x       (12.1)
   ^s_i∈T

В данном случае мы создадим алгоритм перебора с возвратами, печатающий все такие подмножества. Например, если S = {1, 2, 3, 5, 6, 7, 9} и х = 13, то метод должен вывести на экран следующие пять подмножеств: {6, 7}, {2, 5, 6}, {1, 5, 7}, {1, 3, 9} и {1, 2, 3, 7}.

Простейшее решение задачи "в лоб" - это генерация всех возможных подмножеств множества S с проверкой истинности требования (12.1). Такой полный перебор можно осуществить процедурой, подобной generate_subsets() из примера 12.1. Множество S было бы входным списком элементов, а метод имел бы дополнительный параметр, в котором хранится значение х. Кроме этого, процедура в начальном условии перед выводом подмножества на экран должна будет проверить ограничение (12.1). Иными словами, она должна проверять ограничение (12.1) в каждом листе дерева рекурсии.

Однако даже при использовании перебора с возвратами существует возможность ускорить поиск. В примере 12.7 приводится одна из реализаций, где частичное решение (sol) представляет собой подмножество T.

Пример 12.7. Решение задачи о сумме подмножества перебором с возвратами

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

def print_subset_sum(i, sol, psum, elements, x):
    # Базовый вариант
    if psum == x:
        print_subset_binary(sol, elements)
    elif i < len(elements):
        # Генерация элементов-кандидатов
        for k in range(0, 2):

            # Проверить, можно ли обрезать дерево рекурсии
            if psum + k * elements[i] <= x:

                # Расширить частичное решение
                sol[i] = k

                # Обновить сумму, связанную с частичным решением  
                psum = psum + k * elements[i]

                # Попробовать расширить частичное решение
                print_subset_sum(i + 1, sol, psum, elements, x)

                # в этом нет необходимости:
                # psum = psum + k * elements[i]

        # Убедиться, что 0 указывает на отсутствие элемента
        sol[i] = 0


def print_subset_sum_wrapper(elements, x):
    sol = [0] * (len(elements))
    print_subset_sum(0, sol, 0, elements, x)


def print_subset_binary(sol, elements):
    no_elements = True
    print('{', end='')
    for i in range(0, len(sol)):
        if sol[i] == 1:
            if no_elements:
                print(elements[i], sep='', end='')
                no_elements = False
            else:
                print(', ', elements[i], sep='', end='')
    print('}')

Архив с файлом можно взять здесь.

Чтобы избежать вычисления суммы элементов частичного решения в каждом рекурсивном вызове, используется дополнительный параметр - переменная-накопитель суммы psum, которой, очевидно, в методе-оболочке нужно присвоить начальное значение 0. Ключевая идея алгоритма состоит в том, что дерево рекурсии можно сократить, если сумма элементов частичного решения равна х, когда выполнено требование (12.1), или больше х, когда добавление нового положительного целого числа из множества S к частичному решению только увеличивает его сумму (12.1).

Прежде всего метод проверяет начальное условие (строки 3 и 4), когда на экран выводится подмножество (частичное решение), удовлетворяющее ограничению (12.1). Это позволяет сокращать дерево рекурсии в его внутренних узлах глубины i. В начальном условии в T могут входить только первые i элементов S. Другими словами, значимыми являются лишь первые i элементов частичного решения. Если n - i последних элементов могут принимать произвольные значения, то методу печати следовало бы передать значение i и указать "истинный" размер частичного решения. Но вместо этого алгоритм вызывает метод print_subset_binary() из примера 12.1, который требует, чтобы эти последние значения были всегда равны нулю, указывая на то, что они не относятся к частичному решению T. Это требование обеспечивается в методе-оболочке print_subset_sum_wrapper() инициализацией частичного решения n нулями, что равносильно пустому множеству, и обновлением частичного решения таким образом, чтобы последние его n - i элементов всегда оставались нулевыми при достижении начального условия (это реализуется присваиванием в строке 25).

Если частичное решение из n элементов не отвечает требованию (12.1), метод просто завершается, не выполняя никаких действий. В противном случае при выполнении условия i < n (строка 5) он продолжает пополнять частичное решение. В этом случае он использует цикл, где проверяет два варианта - не включать (k = 0) или включать (k = 1) элемент st в частичное решение. Так как k - число, его можно использовать для вычисления суммы psum + k * elements[i] частичного решения. Обратите внимание, что при k = 0 она не меняется, тогда как при k = 1 она увеличивается на s_i. Поэтому перед включением элемента в частичное решение и очередным рекурсивным вызовом в строке 10 проверяется, не превысила ли новая сумма значения х. Если это так, то в частичное решение включается новый кандидат (строка 13), psum обновляется (строка 16) и выполняется рекурсивный вызов (строка 19). После всех этих действий нет необходимости восстанавливать значение psum (в строке 22), так как в первой итерации цикла при k = 0 значение psum не меняется. В завершение алгоритм обнуляет значение позиции i частичного решения, чтобы правильно вывести на экран частичное решение в начальном условии (последние его n - i элементов всегда должны быть нулями).

На рисунке 1 приведено дерево рекурсии метода print_subset_sum() для множества S = {2, 6, 3, 5} и х = 8.

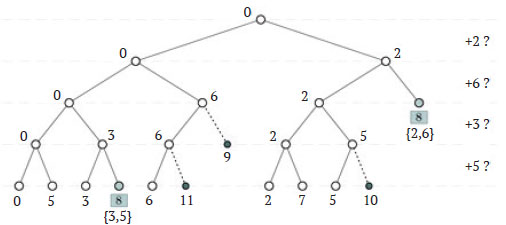
Рис.1. Дерево рекурсии процедуры, решающей задачу суммы подмножества для множества S = {2, 6, 3, 5} и x = 8

Частичные решения создаются на каждом уровне, как в методах, изложенных, начиная с 189 шага. Спускаясь по левой ветви дерева, алгоритм не включает элемент в T, но включает его, спускаясь по правой ветви. Здесь числа рядом с узлами обозначают сумму включенных в частичные решения элементов (psum) при вызове метода. Обратите внимание, что дерево сокращается, как только найдено решение, удовлетворяющее условию (12.1), или сумма элементов в T превысила х.

В итоге вызов print_subset_sum_wrapper([2,6,3,5],8) приводит к правильному результату:

{3, 5}
{2, 6}

В заключение отметим, что без обнуления в строке 25 частичное решение {2, 6} попадёт в начальное условие с единицей в своей третьей позиции, и метод выведет на экран {2, 6, 3}.

На следующем шаге мы рассмотрим путь в лабиринте.

Предыдущий шаг Содержание Следующий шаг