На этом шаге мы рассмотрим представление сети Петри с помощью графов.

В значительной степени теоретическая работа по сетям Петри основана на формальном определении сетей Петри, изложенном на предыдущем шаге. Для иллюстраций понятия сетей Петри более удобно графическое представление сети Петри. Теоретико-графовым представлением сети Петри является двудольный ориентированный мультиграф.

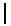Структура сети Петри представляет собой совокупность позиций и переходов. В соответствии с этим граф сети Петри обладает двумя типами узлов. Кружок является позицией, а планка - переходом.

Ориентированные дуги (стрелки) - соединяют позиции и переходы, при этом некоторые дуги направлены от позиций к переходам, а другие - от переходов к позициям. Дуга, направленная от позиции p_i к переходу t_j, определяет позицию, которая является входом перехода. Кратные входы в переход указываются кратными дугами из входных позиций в переход. Выходная позиция указывается дугой из перехода к позиции. Кратные выходы также представлены кратными дугами.

Сеть Петри - это мультиграф, так как он допускает существование кратных дуг от одной вершины графа к другой. Так как дуги являются направленными, то это ориентированный мультиграф. Вершины графа можно разделить на два множества (позиции и переходы) так, что каждая дуга будет направлена от элемента одного множества (позиций или переходов) к элементу другого множества (переходов или позиций). Такой граф является двудольным ориентированным мультиграфом.

Определение.: Граф сети Петри есть двудольный ориентированный мультиграф, G= (V, A), где V = {v₁, v₂, ..., v_s} - множество вершин, а A = {a₁, a₂, ..., a_s} - комплект направленных дуг, a_i=(v_j, v_k), где v_j, v_k принадлежат V. Множество V может быть разбито на два непересекающихся подмножества P и T, таких, что a_i принадлежит A, если a_i = (v_j, v_k), тогда либо v_j принадлежит P и v_k принадлежит T, либо v_j принадлежит T и v_k принадлежит P.

Пример 2. На рисунке 1 изображён граф сети Петри, эквивалентный структуре сети Петри из примера 1 предыдущего шага.

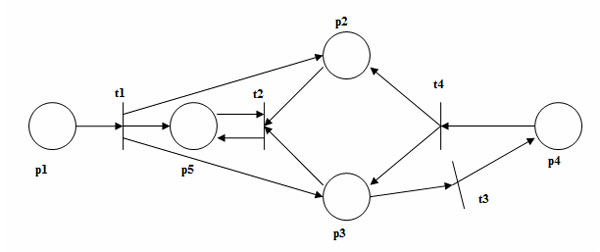
Рис.1. Граф сети Петри

Эти два представления сети Петри - структура сети Петри и граф сети Петри - эквивалентны. Покажем, каким образом можно преобразовать один в другой. Предположим, нам дана структура сети Петри C = (P, T, I, O) с P={p₁, p₂, ... , p_n} и T={ t₁ ,t₂, ... , t_m}. Тогда граф сети Петри можно определить следующим образом.

Определение.

Определим

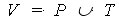. Определим A как комплект направленных дуг, такой, что для всех p_i принадлежит P и t_j принадлежит T

           #((p_i , t_j), A) =  #(p_i ,I(t_j)),
           #((t_j , p_i), A) =  #(p_i ,O(t_j))  .

G = (V, A) есть граф сети Петри, эквивалентный структуре сети Петри C = (P, T, I, O).

Обратное преобразование (от графа сети Петри к структуре) осуществляется подобным образом. Однако при переходе от графа сети Петри к структуре сети Петри возникает интересная задача: если множество вершин можно разделить на два подмножества S и R, то какое из этих подмножеств должно быть позициями, а какое - переходами? Оба возможных варианта позволяют определить сеть Петри, хотя в получающихся в результате структурах позиции и переходы меняются местами.

Двойственной к сети Петри C = (P, T, I, O) является сеть Петри С' = ( T, P, I, O), которая получается в результате перестановки позиций и переходов. Структура графа сохраняется, просто меняются местами кружки и планки.

Пример 3. На рисунке 2 изображена сеть, двойственная сети Петри с рисунка 1.

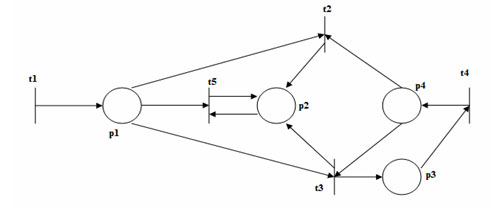
Рис.2. Сеть, двойственная сети Петри, показанной на рисунке 1

Двойственность - полезный приём в теории графов. В исследовании этих сетей никакой пользы извлечь из понятия двойственности сетей Петри нельзя. Это объясняется трудностью определения сети, двойственной к маркированной сети Петри.

На следующем шаге мы рассмотрим маркировку сетей Петри.

Предыдущий шаг Содержание Следующий шаг