На этом шаге мы рассмотрим особенности использования этой модели.

    Рассмотрим, как можно представлять форму трехмерных объектов в системах компьютерной графики. Для описания формы поверхностей могут использоваться разнообразные методы. Сделаем обзор некоторых из них.

Аналитическая модель

    Аналитической моделью будем называть описание поверхности математическими формулами. В компьютерной графике можно использовать много разновидностей такого описания. Например, в виде функции двух аргументов z = f (x, y). Можно использовать уравнение F (x,y,z) = 0.

    Зачастую, используется параметрическая форма описания поверхности. Запишем формулы для трехмерной декартовой системы координат (x,у,z):

  x = Fx (s, t),
  у = Fу (s, t),
  z = Fz (s, t),

    Преимущества параметрического описания - легко описывать поверхности, которые отвечают неоднозначным функциям, замкнутые поверхности. Описание можно сделать таким образом, что формула не будет существенно изменяться при поворотах поверхности, масштабировании.

    В качестве примера рассмотрим аналитическое описание поверхности шара.

    Сначала как функцию двух аргументов:

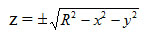
    Затем в виде уравнения: x² + у² + z² = R² = 0.

    А также в параметрической форме:

  x = R sin s cos t,
  y = R sin s sin t,
  z = R cos s.

    Для описания сложных поверхностей часто используют сплайны. Сплайн - это специальная функция, более всего пригодная для аппроксимации отдельных фрагментов поверхности. Несколько сплайнов образовывают модель сложной поверхности. Другими словами, сплайн - эта тоже поверхность, но такая, для которой можно достаточно просто вычислять координаты ее точек. Обычно используют кубические сплайны. Почему именно кубические? Потому, что третья степень - наименьшая из степеней, позволяющих описывать любую форму, и при стыковке сплайнов можно обеспечить непрерывную первую производную - такая поверхность будет без изломов в местах стыка. Сплайны часто задают параметрически. Запишем формулу для компоненты x(s, t) кубического сплайна в виде многочлена третьей степени параметров s и t:

  x (s, t) = a11 s3 t3 + a12 s3t2 + a13s3t  + a14 s3 + 
    + a21 s2 t3 + a22 s2 t2 + a23 s2 t + a24 s2 + 
    + a31 s t3 + a32 s t2 + a33 s t + a34 s + 
    + a41 t3 + a42 t2 + a43 t  + a44. 

    В математической литературе можно ознакомиться со способами определения коэффициентов a_ij для сплайнов, которые имеют заданные свойства. Примеры анализа и синтеза в матричной форме приведены в [1].

    Рассмотрим одну из разновидностей сплайнов - сплайн Безье. Приведем его сначала в обобщенной форме - степени m*n [1]:

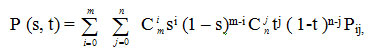
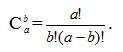
    Кубический сплайн Безье соответствует значениям m = 3, n = 3. для его определения необходимо 16 точек - ориентиров P_ij (рисунок 1); коэффициенты С_mⁱ C_n^j равны 1, 3, 3, 1 при i, j = 0,1,2,3.

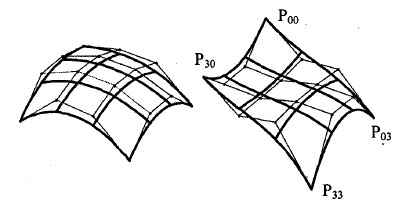
Рис.1. Кубические сплайны Безье

    Характеризуя аналитическую модель в целом, можно сказать, что эта модель наиболее пригодна для многих операций анализа поверхности. С позиций компьютерной графики можно указать такие положительные черты модели: легкая процедура расчета координат каждой точки поверхности, нормали; небольшой объем информации для описания достаточно сложных форм.

    К недостаткам относятся следующие: сложные формулы описания с использованием функций, которые медленно вычисляются на компьютере, снижают скорость выполнения операций отображения; невозможность в большинстве случаев применения данной формы описания непосредственно для построения изображения поверхности. В таких случаях поверхность отображают как многогранник, используя формулы аналитического описания для расчета координат вершин граней в процессе отображения, что уменьшает скорость сравнительно с полигональной моделью описания.

    На следующем шаге мы рассмотрим векторную полигональную модель.

Предыдущий шаг Содержание Следующий шаг