На этом шаге мы рассмотрим многоканальную модель c пуассоновским входным потоком и экспоненциальным распределение длительности обслуживания.
Модель (М / М / с) : (GD/ ∞ / ∞)
Эта модель предусматривает работу с параллельных средств обслуживания. Интенсивность входного потока клиентов равна λ, а интенсивность обслуживания клиентов — μ для каждого сервиса. Поскольку отсутствуют ограничения на количество клиентов в системе, то λэфф = λ.
Результатом использования с параллельных сервисов является пропорциональное увеличение интенсивности обслуживания клиентов системой до nμ, если n ≤ с, и до cμ, если n > с. Следовательно, в терминах общей модели системы обслуживания ( шаг 86) λn и nμn определяются следующим образом.
λn = λ, n ≥ 0,
μn = nμ, n ≤ c,
μn = cμ, n > c.
Следовательно,
pn = [λnp0]/[μ(2μ)(2μ)...(nμ)] = [λnp0]/[n!μn] = (ρn/n!)p0, n ≤ c,
pn = [λnp0]/[μ(2μ)...(c - 1)μ(cμ)n-c+1] = [λnp0]/[c!cn-cμn] = (ρn/(c!cn-c))p0, n > c
Значение вероятности р0 определяется из уравнения ∑pn = 1, n = 0, 1, 2, .... Если ρ = λ/μ, a ρ/c < 1 приходим к следующей формуле для р0:
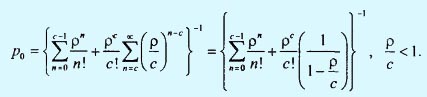
Выражение для Lq можно найти следующим образом.
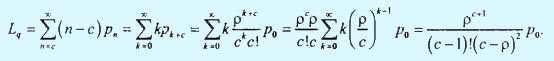
Поскольку λэфф = λ, то Ls = Lq + ρ; значения для Ws и Wq можно найти, разделив на λ значения Ls и Lq .
На следующем шаге рассмотрим применение многоканальной модели c пуассоновским входным потоком.
