На этом шаге мы рассмотрим еще один случай использования PCA.
Впрочем, давайте вернемся к конкретному случаю использования PCA. Мы кратко рассказали о преобразовании PCA как способе поворота данных с последующим удалением компонент, имеющих низкую дисперсию. Еще одна полезная интерпретация заключается в том, чтобы попытаться вычислить значения новых признаков, полученные после поворота PCA, таким образом, мы можем записать тестовые точки в виде взвешенной суммы главных компонент (см. рисунок 1).

Рис.1. Схематическое изображение PCA, осуществляющего разложение изображения на взвешенную сумму компонент
Здесь x1, х2 и т.д. являются коэффициентами главных компонент для конкретной точки данных, другими словами, они представляют собой изображение в новом пространстве, полученном в результате вращения.
Еще один способ понять, что делает модель PCA - реконструировать исходные данные, используя лишь некоторые компоненты. На третьем графике рисунка 1 87 шага мы удалили вторую компоненту, затем мы отменили вращение и добавили обратно среднее значение, чтобы получить новые точки в исходном пространстве с удаленной второй компонентой, как показано на последнем графике того же рисунка 1. Мы можем выполнить аналогичное преобразование для лиц, сократив данные за счет использования лишь некоторых главных компонент и вернувшись затем в исходное пространство. Это возвращение в пространство исходных признаков можно выполнить с помощью метода inverse_transform(). Здесь мы визуализируем результаты реконструкции некоторых лиц, используя 10, 50, 100, 500 и 2000 компонент (рисунок 2):
[In 31]:
mglearn.plots.plot_pca_faces(X_train, X_test, image_shape)
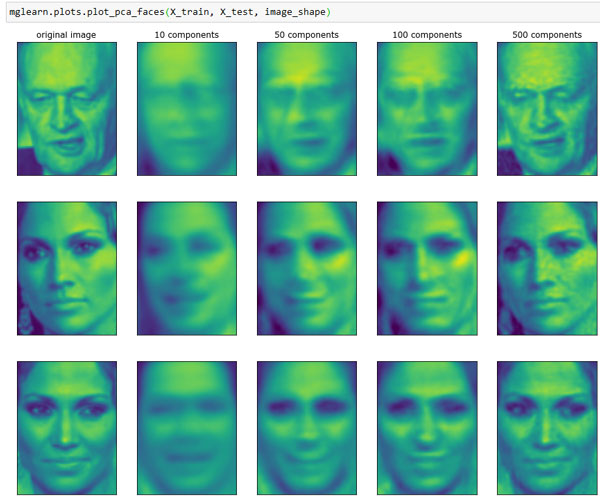
Рис.2. Реконструкция трех изображений лица с помощью постепенного увеличения числа главных компонент
Вы можете увидеть, что, когда мы используем лишь первые 10 главных компонент, фиксируется лишь общая суть картинки, например, ориентация лица и освещенность. По мере увеличения количества используемых компонент сохраняется все больше деталей изображения. Это соответствует включению большего числа слагаемых в сумму, показанную на рисунке 2. Использование числа компонент, равного числу имеющихся пикселей, означало бы, что мы, осуществив поворот, сохранили всю информацию и можем идеально реконструировать изображение.
Кроме того, мы можем применить PCA для визуализации всех лиц набора на диаграмме рассеяния, воспользовавшись первыми двумя главными компонентами (рисунок 3). Для этого мы выделим классы, соответствующие лицам, с помощью определенного цвета и формы (аналогично тому, что делали для набора данных cancer):
[In 32]: mglearn.discrete_scatter(X_train_pca[:, 0], X_train_pca[:, 1], y_train) plt.xlabel("Первая главная компонента") plt.ylabel("Вторая главная компонента") Text(0, 0.5, 'Вторая главная компонента')
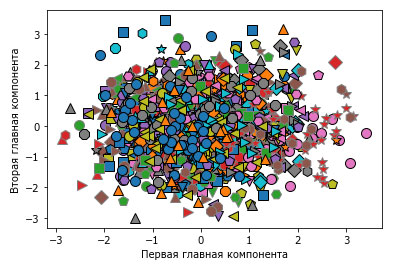
Рис.3. Диаграмма рассеяния для набора лиц, использующая первые две главные компоненты (см. рисунок 2 88 шага с соответствующим изображением для набора данных cancer)
Из рисунка видно, когда мы используем лишь первые две главные компоненты, все данные представляют собой просто одно большое скопление данных без видимого разделения классов. Данный факт неудивителен, учитывая, что даже при использовании 10 компонент, как уже было показано ранее на рисунке 2 этого шага, PCA фиксирует самые общие характеристики лиц.
На следующем шаге мы познакомимся с алгоритмом факторизации неотрицательных матриц [NMF].
