На этом шаге мы рассмотрим использование этого алгоритма для восстановления исходных сигналов.
Допустим, нас интересует сигнал, который представляет собой комбинацию трех различных источников (рисунок 1):
[In 37]: S = mglearn.datasets.make_signals() plt.figure(figsize=(6, 1)) plt.plot(S, '-') plt.xlabel("Время") plt.ylabel("Сигнал")
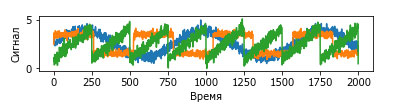
Рис.1. Исходные источники сигнала
К сожалению, мы не можем наблюдать исходные сигналы, лишь аддитивную смесь (сумму) всех трех сигналов. Необходимо восстановить исходные компоненты из этой смеси. Предположим, у нас есть различные способы фиксировать характеристики этого смешанного сигнала (скажем, у нас есть 100 измерительных приборов), каждый из которых дает нам серию измерений:
[In 38]: A = np.random.RandomState(0).uniform(size=(100, 3)) X = np.dot(S, A.T) print("Форма измерений: {}".format(X.shape)) Форма измерений: (2000, 100)
Мы можем использовать NMF, чтобы восстановить три сигнала:
[In 39]: nmf = NMF(n_components=3, random_state=42) S_ = nmf.fit_transform(X) print("Форма восстановленного сигнала: {}".format(S_.shape)) Форма восстановленного сигнала: (2000, 3)
Для сравнения мы еще применим PCA:
[In 40]: pca = PCA(n_components=3) H = pca.fit_transform(X)
Рисунок 2 показывает активность сигнала, обнаруженную с помощью NMF и PCA:
[In 41]: names = ['Наблюдения (первые три измерения)', 'Фактические источники', 'Сигналы, восстановленные NMF', 'Сигналы, восстановленные PCA'] fig, axes = plt.subplots(4, figsize=(8, 4), gridspec_kw={'hspace': .5}, subplot_kw={'xticks': (), 'yticks': ()}) for model, name, ax in zip(models, names, axes): ax.set_title(name) ax.plot(model[:, :3], '-')
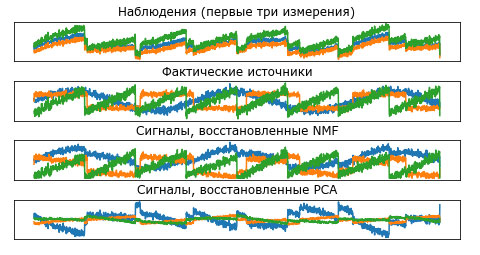
Рис.2. Восстановление первоначальных источников с помощью NMF и PCA
Этот график включает в себя наблюдения по первым 3 измерениям X. Как вы можете увидеть, NMF довольно хорошо выделил первоначальные источники, тогда как PCA потерпел неудачу и использовал первую компоненту, чтобы объяснить большую часть дисперсии данных. Помните о том, что компоненты, полученные с помощью NMF, не упорядочены. В этом примере порядок компонент NMF точно такой же, как в исходном сигнале (см. цвет трех кривых), но это носит чисто случайный характер.
Существует множество других алгоритмов, которые можно использовать для разложения каждой точки данных на взвешенную сумму компонент, как это делают PCA и NMF. Обсуждение всех этих алгоритмов выходит за рамки изложения, а описание ограничений, накладываемых на компоненты и коэффициенты, часто предполагает знание теории вероятностей. Если вас заинтересовал тот или иной алгоритм выделения паттернов, мы рекомендуем вам изучить разделы руководства scikit-learn, посвященные анализу независимых компонент (independent component analysis, ICA), факторному анализу (factor analysis, FA) и разреженному кодированию (sparse coding) с обучением словаря (dictionary learning). Информацию обо всех этих методах можно найти на странице, посвященной декомпозиционным методам.
На следующем шаге мы рассмотрим множественное обучение с помошью алгоритма t-SNE.
