На этом шаге мы рассмотрим использование биннинга.
Оптимальный способ представления данных зависит не только от содержательного смысла данных, но и от вида используемой модели. Линейные модели и модели на основе дерева (например, деревья решений, градиентный бустинг деревьев решений и случайный лес), представляющие собой две большие и наиболее часто используемые группы методов, сильно отличаются друг от друга с точки зрения обработки признаков различных типов. Давайте вернемся к набору данных wave, который мы использовали для регрессионного анализа. Он имеет лишь один входной признак. Ниже приводится сравнение результатов модели линейной регрессии и дерева регрессии для этого набора данных (см. рисунок 1):
[In 11]: from sklearn.linear_model import LinearRegression from sklearn.tree import DecisionTreeRegressor X, y = mglearn.datasets.make_wave(n_samples=100) line = np.linspace(-3, 3, 1000, endpoint=False).reshape(-1, 1) reg = DecisionTreeRegressor(min_samples_split=3).fit(X, y) plt.plot(line, reg.predict(line), label="дерево решений") reg = LinearRegression().fit(X, y) plt.plot(line, reg.predict(line), label="линейная регрессия") plt.plot(X[:, 0], y, 'o', c='k') plt.ylabel("Выход регрессии") plt.xlabel("Входной признак") plt.legend(loc="best")
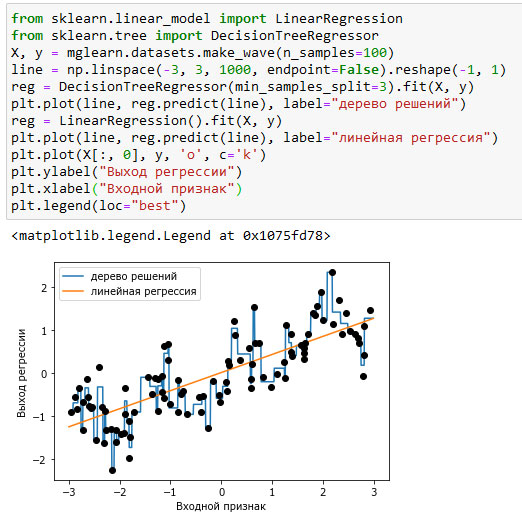
Рис.1. Сравнение результатов модели линейной регрессии и дерева регрессии для набора данных wave
Как вам известно, линейные модели могут моделировать только линейные зависимости, которые представляют собой линии в случае одного признака. Дерево решений может построить гораздо более сложную модель данных. Результаты сильно зависят от представления данных. Одним из способов повысить прогнозную силу линейных моделей при работе с непрерывными данными является биннинг характеристик (binning), также известный как дискретизация (discretization), который разбивает исходный признак на несколько категорий.
Представим, что диапазон значений входного признака (в данном случае от -3 до 3) разбит на определенное количество категорий или бинов (bins), допустим, на 10 категорий. Точка данных будет представлена категорией, в которую она попадает. Сначала мы должны задать категории. В данном случае мы зададим 10 категорий, равномерно распределенных между -3 и 3. Для этого мы используем функцию np.linspace(), создаем 11 элементов, которые дадут 10 категорий - интервалов, ограниченных двумя границами:
[In 12]: bins = np.linspace(-3, 3, 11) print("категории: {}".format(bins)) категории: [-3. -2.4 -1.8 -1.2 -0.6 0. 0.6 1.2 1.8 2.4 3. ]
При этом первая категория содержит все точки данных со значениями признака от -3 до -2.68, вторая категория содержит все точки со значениями признака от -2.68 до -2.37 и так далее.
Далее мы записываем для каждой точки данных категорию, в которую она попадает. Это можно легко вычислить с помощью функции np.digitize():
[In 13]: which_bin = np.digitize(X, bins=bins) print("\nТочки данных:\n", X[:5]) print("\nКатегории для точек данных:\n", which_bin[:5]) Точки данных: [[-0.75275929] [ 2.70428584] [ 1.39196365] [ 0.59195091] [-2.06388816]] Категории для точек данных: [[ 4] [10] [ 8] [ 6] [ 2]]
То, что мы сделали здесь, называется преобразованием непрерывного входного признака набора данных wave в категориальный признак. С помощью категориального признака мы задаем категорию для каждой точки данных. Чтобы запустить модель scikit-learn на этих данных, мы выполним прямое кодирование этого дискретного признака с помощью функции OneHotEncoder() из модуля preprocessing. Функция OneHotEncoder() выполняет ту же самую кодировку, что и pandas.get_dummies(), хотя в настоящее время она работает только с категориальными переменными, которые принимают целочисленные значения:
[In 14]: from sklearn.preprocessing import OneHotEncoder # преобразовываем с помощью OneHotEncoder encoder = OneHotEncoder(sparse=False) # encoder.fit находит уникальные значения, имеющиеся в which_bin encoder.fit(which_bin) # transform осуществляет прямое кодирование X_binned = encoder.transform(which_bin) print(X_binned[:5]) [[0. 0. 0. 1. 0. 0. 0. 0. 0. 0.] [0. 0. 0. 0. 0. 0. 0. 0. 0. 1.] [0. 0. 0. 0. 0. 0. 0. 1. 0. 0.] [0. 0. 0. 0. 0. 1. 0. 0. 0. 0.] [0. 1. 0. 0. 0. 0. 0. 0. 0. 0.]]
Поскольку мы указали 10 категорий, преобразованный набор данных X_binned теперь состоит из 10 признаков:
[In 15]: print("форма массива X_binned: {}".format(X_binned.shape)) форма массива X_binned: (100, 10)
Сейчас мы строим новую модель линеинои регрессии и новую модель дерева решений на основе данных, преобразованных с помощью прямого кодирования. Результат визуализирован на рисунке 2, также показаны границы категорий, обозначенные вертикальными серыми линиями:
[In 16]: line_binned = encoder.transform(np.digitize(line, bins=bins)) reg = LinearRegression().fit(X_binned, y) plt.plot(line, reg.predict(line_binned), label='линейная регрессия после биннинга') reg = DecisionTreeRegressor(min_samples_split=3).fit(X_binned, y) plt.plot(line, reg.predict(line_binned), label='дерево решений после биннинга') plt.plot(X[:, 0], y, 'o', c='k') plt.vlines(bins, -3, 3, linewidth=1, alpha=.2) plt.legend(loc="best") plt.ylabel("Выход регрессии") plt.xlabel("Входной признак")
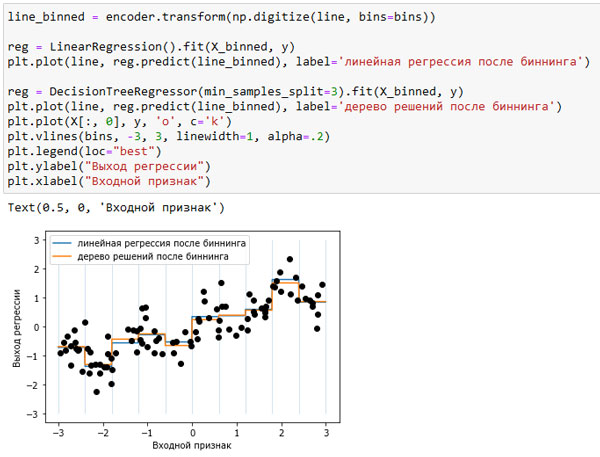
Рис.2. Сравнение результатов модели линейной регрессии и дерева регрессии после проведения биннинга
Синяя и оранжевая линии почти точно лежат поверх друг друга, это означает, что модель линейной регрессии и дерево решений дают почти одинаковые прогнозы. Для каждой категории они предсказывают одно и то же значение (константу). Поскольку признаки принимают почти одно и то же значение в пределах каждой категории, любая модель должна предсказывать почти одно и то же значение для всех точек, находящихся внутри категории. Сравнив модели, обученные до и после биннинга переменных, мы видим, что линейная модель стала теперь гораздо более гибкой, потому что теперь оно присваивает различные значения категориям, в то время как модель дерева решений стала существенно менее гибкой. В целом биннинг признаков не дает положительного эффекта для моделей на основе дерева, поскольку эти модели сами могут научится разбивать данные по любому значению. В некотором смысле это означает, что деревья решений могут самостоятельно осуществить биннинг для наилучшего прогнозирования данных. Кроме того, при выполнении разбиений деревья решений рассматривают несколько признаков сразу, в то время как обычный биннинг выполняется на основе анализа одного признака. Однако линейная модель после преобразования данных выиграла с точки зрения эффективности.
Если есть веские причины использовать линейную модель для конкретного набора данных (например, он имеет большой объем и является многомерным), но некоторые признаки имеют нелинейные взаимосвязи с зависимой переменной - биннинг может быть отличным способом увеличить прогнозную силу модели.
На следующем шаге мы рассмотрим взаимодействия и полиномы.
