На этом шаге мы рассмотрим реализацию такой проверки.

    Как отмечалось ранее, качество модели глубокого обучения никогда не должно оцениваться на обучающих данных - обычно для мониторинга изменения точности модели во время обучения используется проверочная выборка. Создадим такую выборку, включив в нее 10 000 образцов из оригинального набора обучающих данных.

x_val = x_train[:10000]
partial_x_train = x_train[10000:]
y_val = y_train[:10000]
partial_y_train = y_train[10000:]

    Теперь проведем обучение модели в течение 20 эпох (выполнив 20 итераций по всем образцам в обучающей выборке) пакетами по 512 образцов. В то же время будем следить за потерями и точностью по 10 000 отложенных образцов Для этого достаточно передать проверочные данные в аргументе validation_data. Пример 4.7. Обучение модели

history = model.fit(partial_x_train,
                    partial_y_train,
                    epochs=20,
                    batch_size=512,
                    validation_data=(x_val, y_val))

    При использовании CPU на каждую эпоху будет потрачено в среднем 3 секунды. В конце каждой эпохи обучение приостанавливается для вычисления потерь и точности на 10 000 образцах проверочных данных.

    Обратите внимание, что вызов model.fit() возвращает объект History, с которым вы познакомились на 87 шаге. Этот объект имеет поле history - словарь с данными обо всем происходящем в процессе обучения. Заглянем в него:

history_dict = history.history
print(history_dict.keys())

ict_keys(['accuracy', 'loss', 'val_accuracy', 'val_loss'])

    Словарь содержит четыре элемента - по одному на метрику, - за которыми осуществлялся мониторинг в процессе обучения и проверки. В следующих двух примерах используется библиотека Matplotlib для вывода графиков потерь (рисунок 1) и графиков точности на этапах обучения и проверки (рисунок 2). Имейте в виду, что ваши результаты могут несколько отличаться: это обусловлено различием в случайных числах, использовавшихся для инициализации сети.

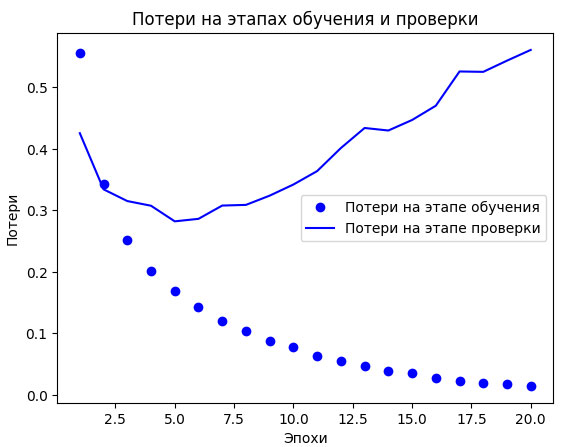
Рис.1. Потери на этапах обучения и проверки

import matplotlib.pyplot as plt

history_dict = history.history
loss_values = history_dict["loss"]
val_loss_values = history_dict["val_loss"]
epochs = range(1, len(loss_values) + 1)
# bo означает blue dot - "синяя точка"
plt.plot(epochs, loss_values, "bo", label="Потери на этапе обучения")
# b означает solid blue line - "сплошная синяя линия"
plt.plot(epochs, val_loss_values, "b", label="Потери на этапе проверки")
plt.title("Потери на этапах обучения и проверки")
plt.xlabel("Эпохи")
plt.ylabel("Потери")
plt.legend()
plt.show()

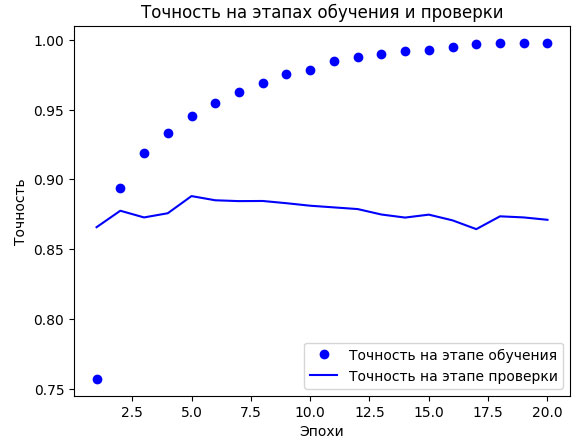
Рис.2. Точность на этапах обучения и проверки

plt.clf() # Очистить рисунок
acc = history_dict["accuracy"]
val_acc = history_dict["val_accuracy"]
plt.plot(epochs, acc, "bo", label="Точность на этапе обучения")
plt.plot(epochs, val_acc, "b", label="Точность на этапе проверки")
plt.title("Точность на этапах обучения и проверки")
plt.xlabel("Эпохи")
plt.ylabel("Точность")
plt.legend()
plt.show()

    Как видите, на этапе обучения потери снижаются с каждой эпохой, а точность растет. Именно такое поведение ожидается от оптимизации градиентным спуском: величина, которую вы пытаетесь минимизировать, должна становиться все меньше с каждой итерацией. Но это не относится к потерям и точности на этапе проверки: похоже, что они достигли пика в четвертую эпоху. Перед вами пример того, о чем мы говорили выше: модель, показывающая хорошие результаты на обучающих данных, не обязательно даст такие же на данных, которые не видела прежде. Выражаясь точнее, в данном случае наблюдается переобучение: после четвертой эпохи произошла чрезмерная оптимизация на обучающих данных - в результате получилось представление, характерное для обучающих данных и не обобщающее данные за пределами обучающего набора.

    В данном случае для предотвращения переобучения можно прекратить обучение после четвертой эпохи. Вообще, есть целый спектр приемов, ослабляющих эффект переобучения, - их мы рассмотрим в следующем разделе.

    А теперь обучим новую модель с нуля в течение четырех эпох и затем оценим получившийся результат на контрольных данных.

model = keras.Sequential([
    layers.Dense(16, activation="relu"),
    layers.Dense(16, activation="relu"),
    layers.Dense(1, activation="sigmoid")
])
model.compile(
    optimizer="rmsprop",
    loss="binary_crossentropy",
    metrics=["accuracy"])
model.fit(x_train, y_train, epochs=4, batch_size=512)
results = model.evaluate(x_test, y_test)

    Конечные результаты:

print(results)

[0.28420743346214294, 0.8865200281143188]

    Первое число (0,29) - это потери на контрольной выборке; второе число (0,89) - точность на контрольной выборке.

    Это простейшее решение позволило достичь точности 89%. При использовании же самых современных подходов точность может доходить до 95%.

    На следующем шаге мы рассмотрим использование обученной сети для предсказаний на новых данных.

Предыдущий шаг Содержание Следующий шаг