На этом шаге мы рассмотрим механизм такого распространения.
На следующей диаграмме представлен пример простой нейронной сети с тремя слоями: входным, скрытым и выходным.
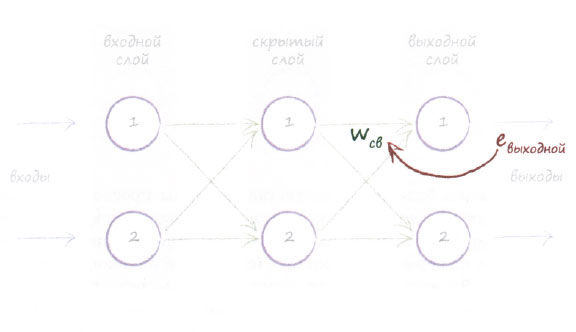
Продвигаясь в обратном направлении от последнего, выходного слоя (крайнего справа), мы видим, как информация об ошибке в выходном слое используется для определения величины поправок к весовым коэффициентам связей, со стороны которых к нему поступают сигналы. Здесь использованы более общие обозначения евыходной для выходных ошибок и wCB для весов связей между скрытым и выходным слоями. Мы вычисляем конкретные ошибки, ассоциируемые с каждой связью, путем распределения ошибки пропорционально соответствующим весам.
Графическое представление позволяет лучше понять, какие вычисления следует выполнить для дополнительного слоя. Мы просто берем ошибки eскрытый на выходе скрытого слоя и вновь распределяем их по предшествующим связям между входным и скрытым слоями пропорционально весовым коэффициентам wBC. Следующая диаграмма иллюстрирует эту логику.
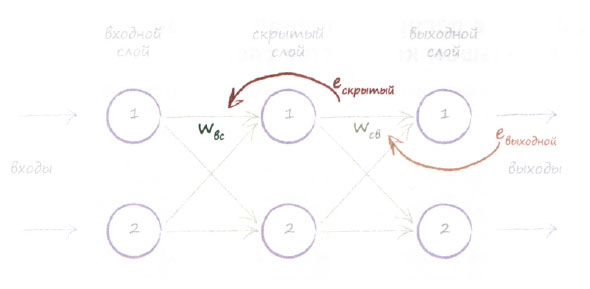
При наличии большего количества слоев мы просто повторили бы описанную процедуру для каждого слоя, продвигаясь в обратном направлении от последнего, выходного слоя. Идея распространения этого потока информации об ошибке (сигнала об ошибке) интуитивно понятна. Вы еще раз имели возможность увидеть, почему этот процесс описывается термином обратное распространение ошибок.
Если мы сначала использовали ошибку евыходной выходного сигнала узлов выходного слоя, то какую ошибку ескрытый мы собираемся использовать для узлов скрытого слоя? Это хороший вопрос, поскольку мы не можем указать очевидную ошибку для узла в таком слое. Из расчетов, связанных с распространением входных сигналов в прямом направлении, мы знаем, что у каждого узла скрытого слоя в действительности имеется только один выход. Вспомните, как мы применяли функцию активации к взвешенной сумме всех входных сигналов данного узла. Но как определить ошибку для такого узла?
У нас нет целевых или желаемых выходных значений для скрытых узлов. Мы располагаем лишь целевыми значениями узлов последнего, выходного слоя, и эти значения происходят из тренировочных примеров. Попытаемся найти вдохновение, взглянув еще раз на приведенную выше диаграмму. С первым узлом скрытого слоя ассоциированы две исходящие из него связи, ведущие к двум узлам выходного слоя. Мы знаем, что можем распределить выходную ошибку между этими связями, поступая точно так же, как и прежде. Это означает, что с каждой из двух связей, исходящих из узла промежуточного слоя, ассоциируется некоторая ошибка. Мы могли бы воссоединить ошибки этих двух связей, чтобы получить ошибку для этого узла в качестве второго наилучшего подхода, поскольку мы не располагаем фактическим целевым значением для узла промежуточного слоя. Следующая диаграмма иллюстрирует эту идею:
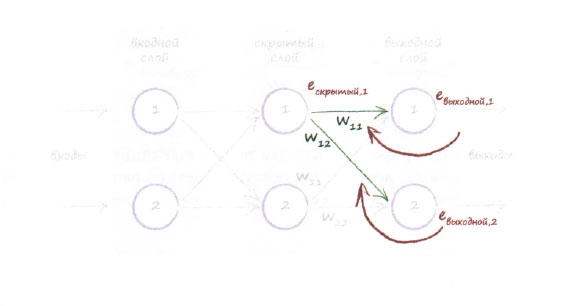
На диаграмме отчетливо видно, что именно происходит, однако для уверенности давайте разберем ее более детально. Нам необходимы величины ошибок для узлов скрытого слоя, чтобы использовать их для обновления весовых коэффициентов связей с предыдущим слоем. Обозначим эти ошибки как ескрытый. Но у нас нет очевидного ответа на вопрос о том, какова их величина. Мы не можем сказать, что ошибка - это разность между желаемым или целевым выходным значением этого узла и его фактическим выходным значением, поскольку данные тренировочного примера предоставляют лишь целевые значения для узлов последнего, выходного слоя. Они не говорят абсолютно ничего о том, какими должны быть выходные сигналы узлов любого другого слоя. В этом и заключается суть сложившейся головоломки.
Мы можем воссоединить ошибки, распределенные по связям, используя обратное распространение ошибок, с которым вы уже познакомились. Поэтому ошибка на первом скрытом узле представляет собой сумму ошибок, распределенных по всем связям, исходящим из этого узла в прямом направлении. На приведенной выше диаграмме показано, что имеется некоторая доля выходной ошибки евыходной1, приписываемая связи с весом w11, и некоторая доля выходной ошибки евыходной2, приписываемая связи с весом w12.
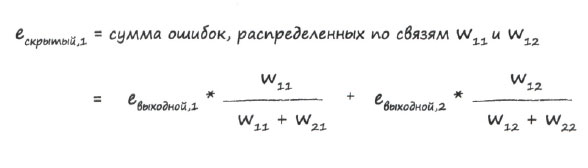
Вышесказанное можно записать в виде следующего выражения:
Чтобы проиллюстрировать, как эта теория выглядит на практике, приведем диаграмму, демонстрирующую обратное распространение ошибок в простой трехслойной сети на примере конкретных данных.
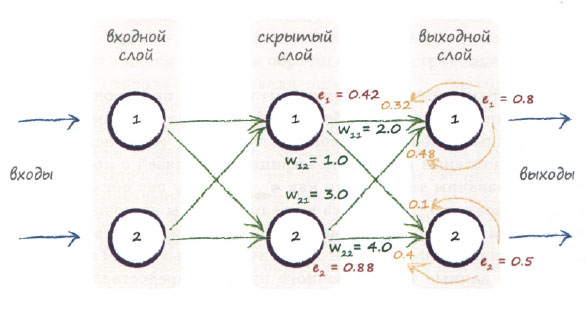
Проследим за обратным распространением одной из ошибок. Вы видите, что после распределения ошибки 0,5 на втором узле выходного слоя между двумя связями с весами 1,0 и 4,0 мы получаем доли, равные 0,1 и 0,4 соответственно. Также можно видеть, что объединенная ошибка на втором узле скрытого слоя представляет собой сумму распределенных ошибок, в данном случае равных 0,48 и 0,4, сложение которых дает 0,88.
На следующей диаграмме демонстрируется применение той же методики к слою, который предшествует скрытому.

Резюме
- Нейронные сети обучаются посредством уточнения весовых коэффициентов своих связей. Этот процесс управляется ошибкой - разностью между правильным ответом, предоставляемым тренировочными данными, и фактическим выходным значением.
- Ошибка на выходных узлах определяется простой разностью между желаемым и фактическим выходными значениями.
- В то же время величина ошибки, связанной с внутренними узлами, не столь очевидна. Одним из способов решения этой проблемы является распределение ошибок выходного слоя между соответствующими связями пропорционально весу каждой связи с последующим объединением соответствующих разрозненных частей ошибки на каждом внутреннем узле.
На следующем шаге мы опишем алгоритм обратного распространения ошибок с помощью матричной алгебры.
