На этом шаге мы рассмотрим использование матричной алгебры для реализации алгоритма обратного распространения ошибок.

Можем ли мы упростить трудоемкие расчеты, используя возможности матричного умножения? Ранее, когда мы проводили расчеты, связанные с распространением входных сигналов в прямом направлении, это нам очень пригодилось.

Чтобы посмотреть, удастся ли нам представить обратное распространение ошибок с помощью более компактного синтаксиса матриц, опишем все шаги вычислительной процедуры, используя матричные обозначения. Кстати, тем самым мы попытаемся векторизовать процесс.

Возможность выразить множество вычислений в матричной форме позволяет нам сократить длину соответствующих выражений и обеспечивает более высокую эффективность компьютерных расчетов, поскольку компьютеры могут использовать повторяющийся шаблон вычислений для ускорения выполнения соответствующих операций.

Отправной точкой нам послужат ошибки, возникающие на выходе нейронной сети в последнем, выходном слое. В данном случае выходной слой содержит только два узла с ошибками e₁ и е₂:

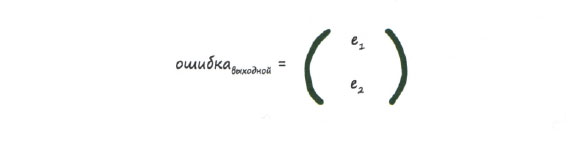
Далее нам нужно построить матрицу для ошибок скрытого слоя. Эта задача может показаться сложной, поэтому мы будем выполнять ее по частям. Первую часть задачи представляет первый узел скрытого слоя. Взглянув еще раз на приведенные выше диаграммы, вы увидите, что ошибка на первом узле скрытого слоя формируется за счет двух вкладов со стороны выходного слоя. Этими двумя сигналами ошибок являются е₁ * w₁₁ / (w₁₁ + w₂₁) и е₂ * w₁₂ / (w₁₂ + w₂₂). А теперь обратите внимание на второй узел скрытого слоя, и вы вновь увидите, что ошибка на нем также формируется за счет двух вкладов: е₁ * w₂₁ / (w₂₁ + w₁₁) и е₂ * w₂₂ / (w₂₂ + w₁₂). Ранее мы уже видели, как работают эти выражения.

Итак, для скрытого слоя мы имеем следующую матрицу, которая выглядит немного сложнее, чем хотелось бы.

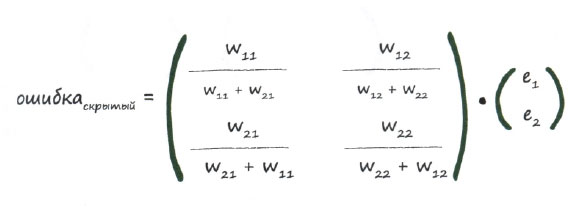
Было бы здорово, если бы это выражение можно было переписать в виде простого перемножения матриц, которыми мы уже располагаем. Это матрицы весовых коэффициентов, прямого сигнала и выходных ошибок. Преимущества, которые можем при этом получить, огромны.

К сожалению, легкого способа превратить это выражение в сверхпростое перемножение матриц, как в случае распространения сигналов в прямом направлении, не существует. Распутать все эти доли, из которых образованы элементы большой матрицы, непросто. Было бы замечательно, если бы мы смогли представить эту матрицу в виде комбинации имеющихся матриц.

Что можно сделать? Нам позарез нужен способ, обеспечивающий возможность использования матричного умножения, чтобы повысить эффективность вычислений.

Ну что ж, дерзнем!

Взгляните еще раз на приведенное выше выражение. Вы видите, что наиболее важная для нас вещь - это умножение выходных ошибок е_n на связанные с ними веса w_ij. Чем больше вес, тем большая доля ошибки передается обратно в скрытый слой. Это важный момент. В дробях, являющихся элементами матрицы, нижняя часть играет роль нормирующего множителя. Если пренебречь этим фактором, можно потерять лишь масштабирование ошибок, передаваемых по механизму обратной связи. Таким образом, выражение е₁ * w₁₁ / (w₁₁ + w₂₁) упростится до е₁ * w₁₁.

Сделав это, мы получим следующее уравнение.

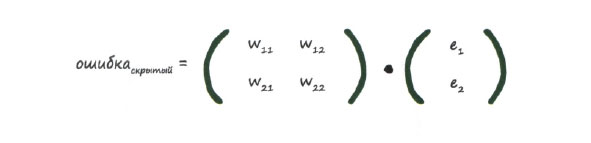
Эта матрица весов напоминает ту, которую мы строили ранее, но она повернута вокруг диагонали, так что правый верхний элемент теперь стал левым нижним, а левый нижний - правым верхним. Такая матрица называется транспонированной и обозначается как w^T.

Ниже приведены два примера транспонирования числовых матриц, которые помогут вам лучше понять смысл операции транспонирования. Вы видите, что она применима даже в тех случаях, когда количество столбцов в матрице отличается от количества строк.

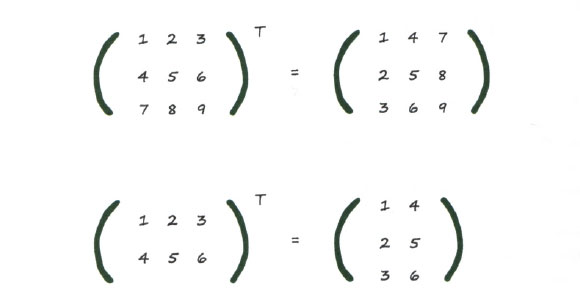
Итак, мы достигли того, чего хотели, - применили матричный подход к описанию обратного распространения ошибок:

Конечно, это просто замечательно, но правильно ли мы поступили, отбросив нормирующий множитель? Оказывается, что эта упрощенная модель обратного распространения сигналов ошибок работает ничуть не хуже, чем более сложная, которую мы разработали перед этим. Если наш простой подход действительно хорошо работает, мы оставим его!

Немного подумав, можно прийти к выводу, что даже в тех случаях, когда в обратном направлении распространяются слишком большие или слишком малые ошибки, сеть сама все исправит при выполнении последующих итераций обучения. Важно то, что при обратном распространении ошибок учитываются весовые коэффициенты связей, и это наилучший показатель того, что мы пытаемся справедливо распределить ответственность за возникающие ошибки.

Мы проделали большую работу, очень большую!

Резюме

Обратное распространение ошибок можно описать с помощью матричного умножения.
Это позволяет нам записывать выражения в более компактной форме, независимо от размеров нейронной сети, и обеспечивает более эффективное и быстрое выполнение вычислений компьютерами, если в языке программирования предусмотрен синтаксис матричных операций.
Отсюда следует, что использование матриц обеспечивает повышение эффективности расчетов как для распространения сигналов в прямом направлении, так и для распространения ошибок в обратном направлении.

Сделайте вполне заслуженный перерыв, поскольку следующий теоретический раздел потребует от вас концентрации внимания и приложения умственных усилий.

На следующем шаге мы поговорим об обновлении весовых коэффициентов.

Предыдущий шаг Содержание Следующий шаг