На этом шаге мы рассмотрим сложности, возникающие при решении этой задачи.
Однако мы пока что не приступили к решению главной задачи - обновлению весов связей в нейронной сети. Мы работали в этом направлении и уже почти достигли намеченной цели. Нам осталось разобрать лишь одну ключевую идею, чтобы больше не было никаких неясностей.
К этому моменту мы научились рассчитывать обратное распространение ошибок до каждого слоя сети. Зачем нам это нужно? Затем, что ошибки подсказывают нам, как должны быть изменены веса связей, чтобы улучшить результирующий общий ответ на выходе нейронной сети. В основном это то, что мы делали с линейным классификатором еще в начале нашего обучения.
Однако узлы - это не простые линейные классификаторы. В узлах сигналы суммируются с учетом весов, после чего к ним применяется сигмоида. Но как нам все-таки справиться с обновлением весов для связей, соединяющих эти более сложные узлы? Почему бы не использовать алгебру для непосредственного вычисления весов?
Последний путь нам не подходит ввиду громоздкости соответствующих выкладок. Существует слишком много комбинаций весов и слишком много функций, зависящих от функций, зависящих от других функций и т.д., которые мы должны комбинировать в ходе анализа распространения сигнала по сети. Представьте себе хотя бы небольшую нейронную сеть с тремя слоями и тремя нейронами в каждом слое, подобную той, с которой мы перед этим работали. Как отрегулировать весовой коэффициент для связи между первым входным узлом и вторым узлом скрытого слоя, чтобы сигнал на выходе третьего узла увеличился, скажем, на 0,5? Даже если бы вам повезло и вы сделали это, достигнутый результат мог бы быть разрушен настройкой другого весового коэффициента, улучшающего сигнал другого выходного узла. Как видите, эти расчеты далеко не тривиальны.
Чтобы убедиться в том, насколько они не тривиальны, достаточно взглянуть на приведенное ниже устрашающее выражение, которое представляет выходной сигнал узла выходного слоя как функцию входных сигналов и весовых коэффициентов связей для простой нейронной сети с тремя слоями по три узла. Входной сигнал на узле i равен хi, весовой коэффициент для связи, соединяющей входной узел i с узлом j скрытого слоя, равен wij. Аналогичным образом выходной сигнал узла j скрытого слоя равен хj, а весовой коэффициент для связи, соединяющей узел j скрытого слоя с выходным узлом k, равен wjk. Необычный символ Σab означает суммирование следующего за ним выражения по всем значениям между а и b.
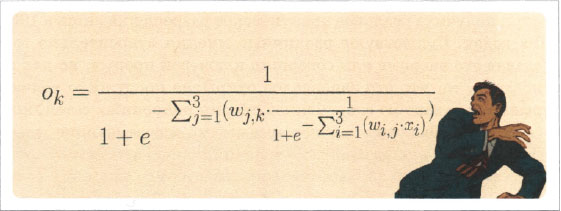
Ничего себе! Лучше держаться от этого подальше.
А не могли бы мы вместо того, чтобы пытаться выглядеть очень умными, просто перебирать случайные сочетания весовых коэффициентов, пока не будет получен устраивающий нас результат?
Этот вопрос не столь уж наивен, как могло бы показаться, особенно когда задача действительно трудная. Такой подход называется методом грубой силы. Некоторые люди пытаются использовать методы грубой силы для того, чтобы взламывать пароли, и это может сработать, если паролем является какое-либо осмысленное слово, причем не очень длинное, а не просто набор символов. Такая задача вполне по силам достаточно мощному домашнему компьютеру. Но представьте, что каждый весовой коэффициент может иметь 1000 возможных значений в диапазоне от -1 до +1, например 0,501, -0,203 или 0,999. Тогда в случае нейронной сети с тремя слоями по три узла, насчитывающей 18 весовых коэффициентов, мы должны были бы протестировать 18 тысяч возможностей. Если бы у нас была более типичная нейронная сеть с 500 узлами в каждом слое, то нам пришлось бы протестировать 500 миллионов различных значений весов. Если бы для расчета каждого набора комбинаций требовалась одна секунда, то для обновления весов с помощью всего лишь одного тренировочного примера понадобилось бы примерно 16 лет. Тысяча тренировочных примеров - и мы имели бы 16 тысяч лет!
Как видите, подход, основанный на методе грубой силы, практически нереализуем. В действительности по мере добавления в сеть новых слоев, узлов или вариантов перебора весов ситуация очень быстро ухудшается.
Эта головоломка не поддавалась математикам на протяжении многих лет и получила реальное практическое разрешение лишь в 1960-1970-х годах. Существуют различные мнения относительно того, кто сделал это впервые или совершил ключевой прорыв, но для нас важно лишь то, что это запоздалое открытие послужило толчком к взрывному развитию современной теории нейронных сетей, которая сейчас способна решать некоторые весьма впечатляющие задачи.
Но все же, как нам разрешить эту явно трудную проблему? Хотите верьте, хотите нет, но вы уже владеете средствами, с помощью которых сможете справиться с этим самостоятельно. Все, что вам для этого нужно знать, мы уже обсуждали. Теперь можем продолжить.
Самое главное, что требуется от нас, - это не бояться пессимизма.
Математические выражения, позволяющие определить выходной сигнал нейронной сети при известных весовых коэффициентах, необычайно сложны, и в них нелегко разобраться. Количество различных комбинаций слишком велико для того, чтобы пытаться тестировать их поочередно.
Для пессимизма есть и ряд других причин. Тренировочных данных может оказаться недостаточно для эффективного обучения сети. В тренировочных данных могут быть ошибки, в связи с чем справедливость нашего предположения о том, что они истинны и на них можно учиться, оказывается под вопросом. Количество слоев или узлов в самой сети может быть недостаточным для того, чтобы правильно моделировать решение задачи.
Это означает, что предпринимаемый нами подход должен быть реалистичным и учитывать указанные ограничения. Если мы будем следовать этим принципам, то, возможно, найдем решение, которое, даже не будучи идеальным с математической точки зрения, даст нам лучшие результаты, поскольку не будет основано на ложных идеалистических допущениях.
На следующем шаге мы продолжим изучение этого вопроса.
