На этом шаге мы рассмотрим метод градиентного спуска.

Проиллюстрируем суть наших рассуждений на следующем примере. Представьте себе ландшафт с очень сложным рельефом, имеющим возвышения и впадины, а также холмы с предательскими буграми и ямами. Вокруг так темно, что ни зги не видно. Вы знаете, что находитесь на склоне холма, и вам нужно добраться до его подножия. Точной карты местности у вас нет. Но у вас есть фонарь. Что вы будете делать? Пожалуй, вы воспользуетесь фонарем и осмотритесь вокруг себя. Света фонаря не хватит для дальнего обзора, и вы наверняка не сможете осмотреть весь ландшафт целиком. Но вы сможете увидеть, по какому участку проще всего начать спуск к подножию холма, и сделаете несколько небольших шагов в этом направлении. Действуя подобным образом, вы будете медленно, шаг за шагом, продвигаться вниз, не располагая общей картой и заблаговременно проложенным маршрутом.

Математическая версия этого подхода называется методом градиентного спуска, и причину этого нетрудно понять. После того как вы сделали шаг в выбранном направлении, вы вновь осматриваетесь, чтобы увидеть, какой путь ведет вас к цели, и делаете очередной шаг в этом направлении. Вы продолжаете действовать точно так же до тех пор, пока благополучно не спуститесь к подножию холма.

А теперь представьте, что этим сложным ландшафтом является математическая функция. Метод градиентного спуска позволяет находить минимум, даже не располагая знаниями свойств этой функции, достаточными для нахождения минимума математическими методами. Если функция настолько сложна, что простого способа нахождения минимума алгебраическими методами не существует, то мы можем вместо этого применить метод градиентного спуска. Ясное дело, он может не дать нам точный ответ, поскольку мы приближаемся к ответу шаг за шагом, постепенно улучшая нашу позицию. Но это лучше, чем вообще не иметь никакого ответа. Во всяком случае, мы можем продолжить уточнение ответа еще более мелкими шагами по направлению к минимуму, пока не достигнем желаемой точности.

А какое отношение имеет этот действительно эффективный метод градиентного спуска к нейронным сетям? Если упомянутой сложной функцией является ошибка сети, то спуск по склону для нахождения минимума означает, что мы минимизируем ошибку. Мы улучшаем выходной сигнал сети. Это именно то, чего мы хотим!

Чтобы вы все наглядно усвоили, рассмотрим использование метода градиентного спуска на простейшем примере.

Ниже приведен график простой функции у = (х - 1)² + 1. Если бы это была функция, описывающая ошибку, то мы должны были бы найти значение х, которое минимизирует эту функцию. Представим на минуту, что мы имеем дело не со столь простой функцией, а с гораздо более сложной.

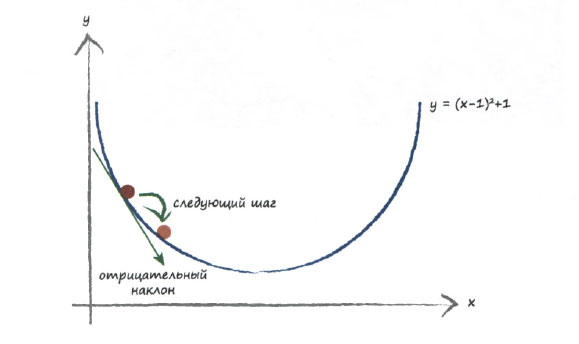
Градиентный спуск должен с чего-то начинаться. На графике показана случайно выбранная начальная точка. Подобно покорителю гор, мы исследуем место, в котором находимся, и видим, в каком направлении идет спуск. Наклон кривой также обозначен на графике, и в данном случае ему соответствует отрицательный градиент. Мы хотим следовать в направлении вниз, поэтому движемся вдоль оси х вправо. Таким образом, мы немного увеличиваем х. Это первый шаг нашего альпиниста. Вы видите, что мы улучшили нашу позицию и продвинулись ближе к фактическому минимуму.

Представим, что мы начали спуск с какого-то другого места, как показано на следующем графике.

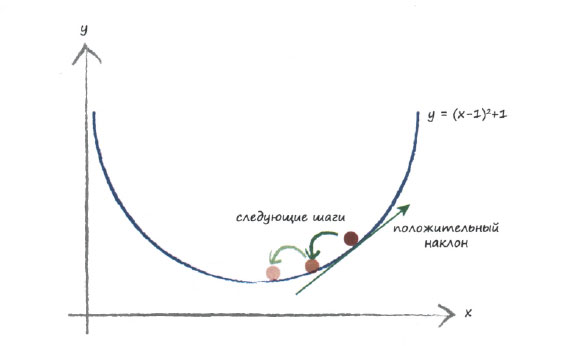
На этот раз наклон почвы под нашими ногами положителен, поэтому мы движемся влево, т.е. немного уменьшаем х. И вновь вы видите, что мы улучшили наше положение, приблизившись к фактическому минимуму. Мы можем продолжать действовать в том же духе до тех пор, пока изменения не станут настолько малыми, что мы будем считать, что достигли минимума.

Необходимым усовершенствованием этого метода должно быть изменение величины шагов во избежание перескока через минимум, что приведет к бесконечным прыжкам вокруг него. Вообразите, что мы оказались на расстоянии 0,5 метра от истинного минимума, но длина нашего шага всегда равна 2 метра. Тогда мы будем постоянно пропускать минимум, поскольку на каждом шаге в его направлении мы будем перескакивать через него. Если мы будем уменьшать величину шага пропорционально величине градиента, то по мере приближения к минимуму будем совершать все более мелкие шаги. При этом мы предполагаем, что чем ближе к минимуму, тем меньше наклон. Для большинства гладких (непрерывно дифференцируемых) функций такое предположение вполне приемлемо. Оно не будет справедливым лишь по отношению к экзотическим зигзагообразным функциям со взлетами и провалами в точках, которые математики называют точками разрыва.

Идея уменьшения величины шага по мере уменьшения величины градиента, являющейся хорошим индикатором близости к минимуму, иллюстрируется следующим графиком.

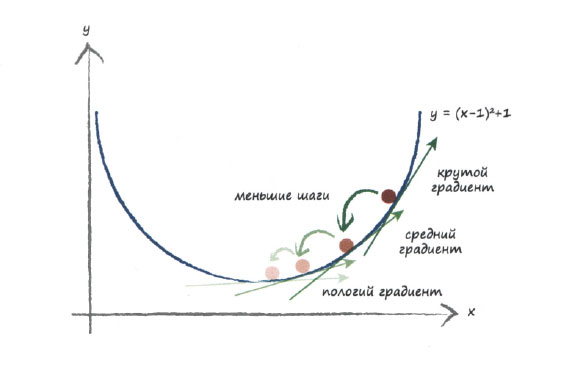
Кстати, обратили ли вы внимание на то, что мы изменяем х в направлении, противоположном направлению градиента? Положительный градиент означает, что мы должны уменьшить х. Отрицательный градиент требует увеличения х. Все это отчетливо видно на графике, но это легко упустить из виду и пойти совершенно неправильным путем.

Используя метод градиентного спуска, мы не пытались находить истинный минимум алгебраическим методом, поскольку сделали вид, будто функция у = (х - 1)² + 1 для этого слишком сложна. Даже если бы мы не могли определить наклон кривой с математической точностью, мы могли бы оценить его, и, как нетрудно заметить, это все равно вело бы нас в правильном общем направлении.

Вся мощь этого метода по-настоящему проявляется в случае функций, зависящих от многих параметров. Например, вместо зависимости у от х мы можем иметь зависимость от a, b, с, d, е и f. Вспомните, что функция выходного сигнала, а вместе с ней и функция ошибки зависят от множества весовых коэффициентов, которые часто исчисляются сотнями!

Следующий график вновь иллюстрирует метод градиентного спуска, но на этот раз применительно к более сложной функции, зависящей от двух параметров. График такой функции можно представить в трех измерениях, где высота представляет значение функции.

Возможно, глядя на эту трехмерную поверхность, вы задумались над тем, может ли метод градиентного спуска привести в другую долину, которая расположена справа. В действительности этот вопрос можно обобщить: не приводит ли иногда метод градиентного спуска в ложную долину, поскольку некоторые сложные функции имеют множество долин?

Что такое ложная долина? Это долина, которая не является самой глубокой. Тогда на поставленный вопрос следует дать утвердительный ответ: да, такое может происходить.

На следующей иллюстрации показаны три варианта градиентного спуска, один из которых приводит к ложному минимуму.

Давайте немного передохнем и соберемся с мыслями.

Резюме

Метод градиентного спуска - это действительно хороший способ нахождения минимума функции, и он прекрасно работает, когда функция настолько сложна, что ее математическая обработка алгебраическими методами сопряжена с большими трудностями.
Более того, этот метод хорошо работает в случае функций многих переменных, когда другие методы не срабатывают либо их невозможно реализовать на практике.
Данный метод также устойчив к наличию дефектных данных и не заведет вас далеко в неправильную сторону, если функция не описывается идеально или же время от времени мы совершаем неверные шаги.

На следующем шаге мы продолжим изучение этого вопроса.

Предыдущий шаг Содержание Следующий шаг