На этом шаге мы обоснуем необходимость использования дифференциального исчисления.
Выходной сигнал нейронной сети представляет собой сложную, трудно поддающуюся описанию функцию со многими параметрами, весовыми коэффициентами связей, которые влияют на выходной сигнал. Так можем ли мы использовать метод градиентного спуска для определения подходящих значений весов? Можем, если правильно выберем функцию ошибки.
Функция выходного сигнала сама по себе не является функцией ошибки. Но мы знаем, что можем легко превратить ее в таковую, поскольку ошибка - это разность между целевыми тренировочными значениями и фактическими выходными значениями.
Однако здесь есть кое-что, чего следует остерегаться. Взгляните на приведенную ниже таблицу с тренировочными данными и фактическими значениями для трех выходных узлов вместе с кандидатами на роль функции ошибок.
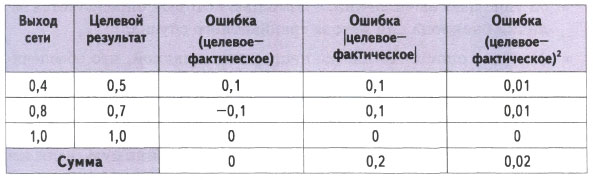
Нашим первым кандидатом на роль функции ошибки является простая разность значений (целевое - фактическое). Это кажется вполне разумным, не так ли? Но если вы решите использовать сумму ошибок по всем узлам в качестве общего показателя того, насколько хорошо обучена сеть, то эта сумма равна нулю!
Что случилось? Ясно, что сеть еще недостаточно натренирована, поскольку выходные значения двух узлов отличаются от целевых значений. Но нулевая сумма означает отсутствие ошибки. Это объясняется тем, что положительная и отрицательная ошибки взаимно сократились. Отсюда следует, что простая разность значений, даже если бы их взаимное сокращение было неполным, не годится для использования в качестве меры величины ошибки.
Пойдем другим путем, взяв абсолютную величину разности. Формально это записывается как |целевое-фактическое| и означает, что знак результата вычитания игнорируется. Это могло бы сработать, поскольку в данном случае ничто ни с чем не может сократиться. Причина, по которой данный метод не получил популярности, связана с тем, что при этом наклон не является непрерывной функцией вблизи минимума, что затрудняет использование метода градиентного спуска, поскольку мы будем постоянно совершать скачки вокруг V-образной долины, характерной для функции ошибки подобного рода. При приближении к минимуму наклон, а вместе с ним и величина шага изменения переменной, не уменьшается, а это означает риск перескока.
Третий вариант заключается в том, чтобы использовать в качестве меры ошибки квадрат разности: (целевое-фактическое)2. Существует несколько причин, по которым третий вариант предпочтительнее второго, включая следующие:
- он упрощает вычисления, с помощью которых определяется величина наклона для метода градиентного спуска;
- функция ошибки является непрерывно гладкой, что обеспечивает нормальную работу метода градиентного спуска ввиду отсутствия провалов и скачков значений функции;
- по мере приближения к минимуму градиент уменьшается, что означает снижение риска перескока через минимум, если используется уменьшение величины шагов.
А возможны ли другие варианты? Да, вы вправе сконструировать любую сложную функцию, которую считаете нужной. Одни из них могут вообще не работать, другие могут хорошо работать для определенного круга задач, а третьи могут работать действительно хорошо, но их чрезмерная сложность приводит к неоправданным затратам ресурсов.
А тем временем мы вышли на финишную прямую!
Чтобы воспользоваться методом градиентного спуска, нам нужно определить наклон функции ошибки по отношению к весовым коэффициентам. Это требует применения дифференциального исчисления. Дифференциальное исчисление - это просто математически строгий подход к определению величины изменения одних величин при изменении других. Например, оно позволяет ответить на вопрос о том, как изменяется длина пружины в зависимости от величины усилия, приложенного к ее концам. В данном случае нас интересует зависимость функции ошибки от весовых коэффициентов связей внутри нейронной сети. Иными словами, нас интересует, насколько величина ошибки чувствительна к изменениям весовых коэффициентов.
Начнем с рассмотрения графика, поскольку это всегда позволяет почувствовать под ногами твердую почву, когда пытаешься решать трудную задачу.
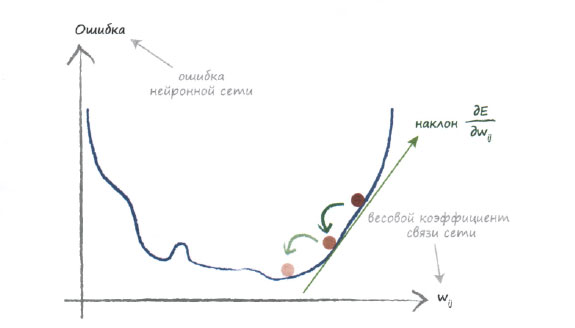
Этот график в точности повторяет один из тех, которые приводились ранее, чтобы подчеркнуть, что мы не делаем ничего принципиально нового. На этот раз функцией, которую мы пытаемся минимизировать, является ошибка на выходе нейронной сети. В этом простом примере показан лишь один весовой коэффициент, но мы знаем, что в нейронных сетях их будет намного больше.
На следующей диаграмме отображаются два весовых коэффициента, и поэтому функция ошибки графически отображается в виде трехмерной поверхности, высота расположения точек которой изменяется с изменением весовых коэффициентов связей. Как видите, теперь процесс минимизации ошибки больше напоминает спуск в долину по рельефной местности.
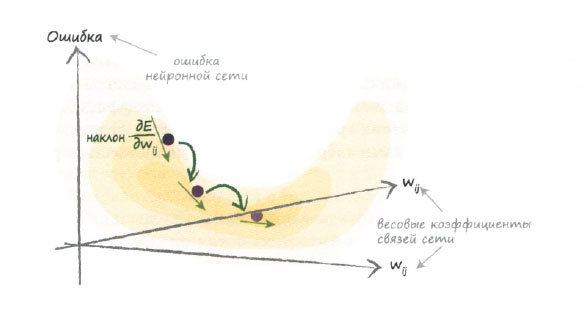
Визуализировать многомерную поверхность ошибки как функции намного большего количества параметров значительно труднее, но идея нахождения минимума методом градиентного спуска остается той же.
Сформулируем на языке математики, чего мы хотим:

Это выражение представляет изменение ошибки Е при изменении веса wjk. Это и есть тот наклон функции ошибки, который нам нужно знать, чтобы начать градиентный спуск к минимуму.
Прежде чем мы развернем это выражение, временно сосредоточим внимание только на весовых коэффициентах связей между скрытым слоем и последним выходным слоем. Интересующая нас область выделена на приведенной ниже диаграмме. К связям между входным и скрытым слоями мы вернемся позже.
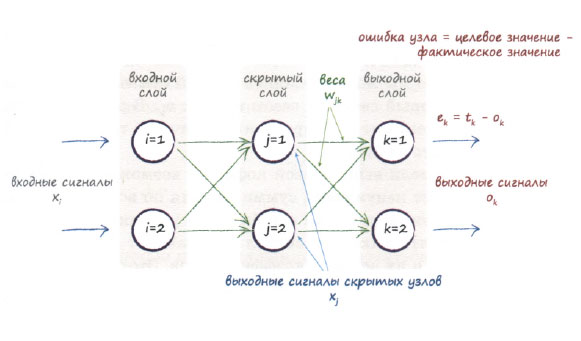
Мы будем постоянно ссылаться на эту диаграмму, дабы в процессе вычислений не забыть о том, что в действительности означает каждый символ. Пусть вас это не смущает, поскольку шаги вычислительной процедуры не являются сложными и будут объясняться, а все необходимые понятия ранее уже обсуждались.
На следующем шаге мы закончим изучение этого вопроса.
