На этом шаге мы закончим изучение этого вопроса.

Прежде всего запишем в явном виде функцию ошибки, которая представляет собой сумму возведенных в квадрат разностей между целевым и фактическим значениями, где суммирование осуществляется по всем n выходным узлам.

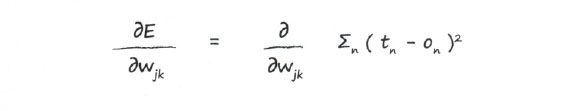
Здесь мы всего лишь записали, что на самом деле представляет собой функция ошибки Е.

Мы можем сразу же упростить это выражение, заметив, что выходной сигнал о_n на узле n зависит лишь от связей, которые с ним соединены. Для узла k это означает, что выходной сигнал о_k зависит лишь от весов w_jk, поскольку эти веса относятся к связям, ведущим к узлу k.

Это можно рассматривать еще и как то, что выходной сигнал узла k не зависит от весов w_jb, где b не равно k, поскольку связь между этими узлами отсутствует. Вес w_jb относится к связи, ведущей к выходному узлу b, но не k.

Это означает, что мы можем удалить из этой суммы все сигналы о_n кроме того, который связан с весом w_jk, т.е. о_k. В результате мы полностью избавляемся от суммирования! Отличный трюк, который вам стоит запомнить на будущее.

Если вы уже успели выпить свой кофе, то, возможно, сообразили, что это означает ненужность суммирования по всем выходным узлам для нахождения функции ошибки. Мы уже видели, чем это объясняется: тем, что выходной сигнал узла зависит лишь от ведущих к нему связей и их весовых коэффициентов. Этот момент часто остается нераскрытым во многих учебниках, которые просто приводят выражение для функции без каких-либо пояснений.

Как бы то ни было, теперь мы имеем более простое выражение:

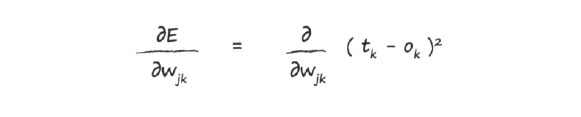
А сейчас мы используем некоторые средства дифференциального исчисления.

Член t_k - константа и поэтому не изменяется при изменении w_jk, т.е. не является функцией w_jk. Было бы очень странно, если бы истинные примеры, предоставляющие целевые значения, изменялись в зависимости от весовых коэффициентов! В результате у нас остается член о_k, который, как мы знаем, зависит от w_jk, поскольку весовые коэффициенты влияют на распространение в прямом направлении сигналов, которые затем превращаются в выходные сигналы о_k.

Чтобы разбить эту задачу дифференцирования на более простые части, мы воспользуемся цепным правилом (правило дифференцирования сложных функций).

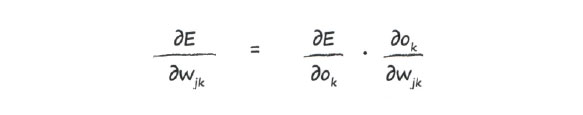
Теперь мы можем разделаться с каждой из этих частей по отдельности. С первой частью мы справимся легко, поскольку для этого нужно всего лишь взять простую производную от квадратичной функции. В результате получаем:

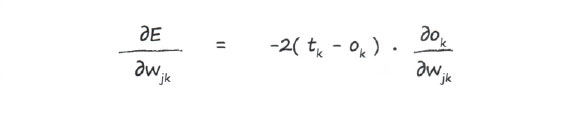
Со второй частью придется немного повозиться, но и это не вызовет больших затруднений. Здесь о_k - это выходной сигнал узла k, который, как вы помните, получается в результате применения сигмоиды к сигналам, поступающим на данный узел. Для большей ясности запишем это в явном виде:

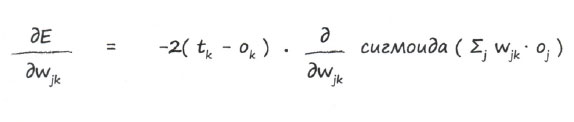
Здесь о_j - выходной сигнал узла предыдущего скрытого слоя, а не выходной сигнал узла последнего слоя.

Как продифференцировать сигмоиду? Мы могли бы это сделать самостоятельно, проведя сложные и трудоемкие вычисления в соответствии с известными фундаментальными идеями, однако эта работа уже проделана другими людьми. Поэтому мы просто воспользуемся уже известным ответом, как это ежедневно делают математики по всему миру.

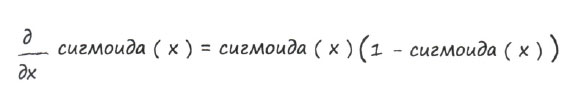
Дифференцирование некоторых функций приводит к выражениям устрашающего вида. В случае же сигмоиды результат получается очень простым. Это одна из причин широкого применения сигмоиды в качестве функции активации в нейронных сетях.

Используя этот впечатляющий результат, получаем следующее выражение:

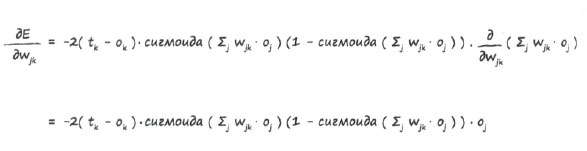
А откуда взялся последний сомножитель? Это результат применения цепного правила к производной сигмоиды, поскольку выражение под знаком функции сигмоида() также должно быть продифференцировано по переменной w_jk. Это делается очень просто и дает в результате o_j.

Прежде чем записать окончательный ответ, избавимся от множителя 2 в начале выражения. Мы вправе это сделать, поскольку нас интересует только направление градиента функции ошибки, так что этот множитель можно безболезненно отбросить. Нам совершенно безразлично, какой множитель будет стоять в начале этого выражения, 2, 3 или даже 100, коль скоро мы всегда будем его игнорировать. Поэтому для простоты избавимся от него.

Окончательное выражение, которое мы будем использовать для изменения веса w_jk, выглядит так.

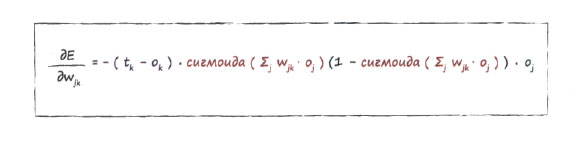
Ух ты! У нас все получилось!

Это и есть то магическое выражение, которое мы искали. Оно является ключом к тренировке нейронных сетей.

Проанализируем вкратце это выражение, отдельные части которого выделены цветом. Первая часть, с которой вы уже хорошо знакомы, - это ошибка (целевое значение минус фактическое значение). Сумма, являющаяся аргументом сигмоиды, - это сигнал, поступающий на узел выходного слоя, и для упрощения вида выражения мы могли бы обозначить этот сигнал просто как i_k. Он выступает в качестве входного сигнала узла k до применения функции активации. Последняя часть - это выходной сигнал узла j предыдущего скрытого слоя. Рассмотрение полученного выражения именно в таком ракурсе позволяет лучше понять связь физической картины происходящего с наклоном функции и в конечном счете с уточнением весовых коэффициентов.

Это поистине фантастический результат, и мы можем заслуженно гордиться собой. Путь к этому результату многим людям дается с большим трудом.

Нам осталось сделать совсем немного, и мы достигнем цели. Выражение, с которым мы совладали, предназначено для уточнения весовых коэффициентов связей между скрытым и выходным слоями. Мы должны завершить работу и найти наклон аналогичной функции ошибки для коэффициентов связей между входным и скрытым слоями.

Можно было бы вновь произвести полностью все математические выкладки, но мы не будем этого делать. Мы воспользуемся описанной перед этим физической интерпретацией составляющих выражения для производной и реконструируем его для интересующего нас нового набора коэффициентов. При этом необходимо учесть следующие изменения.

Первая часть выражения для производной, которая ранее была выходной ошибкой (целевое значение минус фактическое значение), теперь становится рекомбинированной выходной ошибкой скрытых узлов, рассчитываемой в соответствии с механизмом обратного распространения ошибок, с чем вы уже знакомы. Назовем ее е_j.
Вторая часть выражения, включающая сигмоиду, остается той же, но выражение с суммой, передаваемое функции, теперь относится к предыдущим слоям, и поэтому суммирование осуществляется по всем входным сигналам скрытого слоя, сглаженным весами связей, ведущих к скрытому узлу j. Мы могли бы назвать эту сумму i_j.
Последняя часть выражения приобретает смысл выходных сигналов o_i узлов первого слоя, и в данном случае эти сигналы являются входными.

Тем самым нам удалось изящно избежать излишних трудоемких вычислений, в полной мере воспользовавшись всеми преимуществами симметрии задачи для конструирования нового выражения. Несмотря на всю ее простоту, это очень мощная методика, взятая на вооружение выдающимися математиками и учеными. Овладев ею, вы, несомненно, произведете на коллег большое впечатление!

Итак, вторая часть окончательного ответа, к получению которого мы стремимся (градиент функции ошибки по весовым коэффициентам связей между входным и скрытым слоями), приобретает следующий вид:

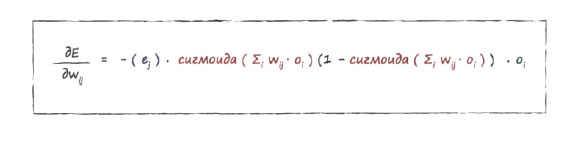
На данном этапе нами получены все ключевые магические выражения, необходимые для вычисления искомого градиента, который мы используем для обновления весовых коэффициентов по результатам обучения на каждом тренировочном примере, чем мы сейчас и займемся.

Не забывайте о том, что направление изменения коэффициентов противоположно направлению градиента, что неоднократно демонстрировалось на предыдущих диаграммах. Кроме того, мы сглаживаем интересующие нас изменения параметров посредством коэффициента обучения, который можно настраивать с учетом особенностей конкретной задачи. С этим подходом вы также уже сталкивались, когда при разработке линейных классификаторов мы использовали его для уменьшения негативного влияния неудачных примеров на эффективность обучения, а при минимизации функции ошибки - для того, чтобы избежать постоянных перескоков через минимум. Выразим это на языке математики:

Обновленный вес w_jk - это старый вес с учетом отрицательной поправки, величина которой пропорциональна производной функции ошибки. Поправка записана со знаком "минус", поскольку мы хотим, чтобы вес увеличивался при отрицательной производной и уменьшался при положительной, о чем ранее уже говорилось. Символ α (альфа) - это множитель, сглаживающий величину изменений во избежание перескоков через минимум. Этот коэффициент часто называют коэффициентом обучения.

Данное выражение применяется к весовым коэффициентам связей не только между скрытым и выходным, но и между входным и скрытым слоями. Эти два случая различаются градиентами функции ошибки, выражения для которых приводились выше.

Прежде чем закончить с этим примером, посмотрим, как будут выглядеть те же вычисления в матричной записи. Для этого сделаем то, что уже делали раньше, - запишем, что собой представляет каждый элемент матрицы изменений весов.

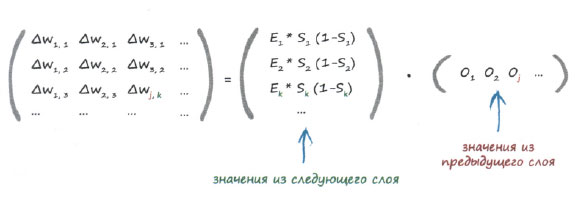
Мы опустили коэффициент обучения α, поскольку это всего лишь константа, которая никак не влияет на то, как мы организуем матричное умножение.

Матрица изменений весов содержит значения поправок к весовым коэффициентам w_jk для связей между узлом j одного слоя и узлом k следующего слоя. Вы видите, что в первой части выражения справа от знака равенства используются значения из следующего слоя (узел k), а во второй - из предыдущего слоя (узел j).

Возможно, глядя на приведенную выше формулу, вы заметили, что горизонтальная матрица, представленная одной строкой, - это транспонированная матрица сигналов о_j, на выходе предыдущего слоя. Цветовое выделение элементов матриц поможет вам понять, что скалярное произведение матриц отлично работает и в этом случае.

Используя символическую запись матриц, мы можем привести эту формулу к следующему виду, хорошо приспособленному для реализации в программном коде на языке, обеспечивающем эффективную работу с матрицами.

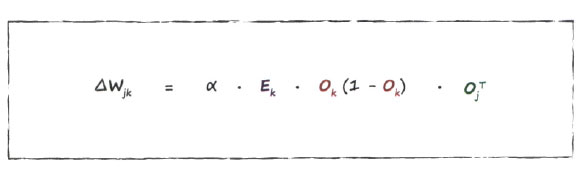
Фактически это выражение совсем не сложное. Сигмоиды исчезли из поля зрения, поскольку они скрыты в матрицах выходных сигналов ок узлов.

Вот и все! Работа сделана.

Резюме

Ошибка нейронной сети является функцией весов внутренних связей.
Улучшение нейронной сети означает уменьшение этой ошибки посредством изменения указанных весов.
Непосредственный подбор подходящих весов наталкивается на значительные трудности. Альтернативный подход заключается в итеративном улучшении весовых коэффициентов путем уменьшения функции ошибки небольшими шагами. Каждый шаг совершается в направлении скорейшего спуска из текущей позиции. Этот подход называется градиентным спуском.
Градиент ошибки можно без особых трудностей рассчитать, используя дифференциальное исчисление.

На следующем шаге мы рассмотрим пример обновления весовых коэффициентов.

Предыдущий шаг Содержание Следующий шаг