На этом шаге мы рассмотрим такой пример.

Проиллюстрируем применение описанного метода обновления весовых коэффициентов на конкретном примере с использованием числовых данных.

С представленной ниже сетью мы уже работали, но в этот раз будут использованы заданные значения выходных сигналов первого и второго узлов скрытого слоя, o_j=1 и o_j=2. Эти значения лишь иллюстрируют применение методики и выбраны произвольно, а не вычислены, как это следовало бы сделать, по известным выходным сигналам

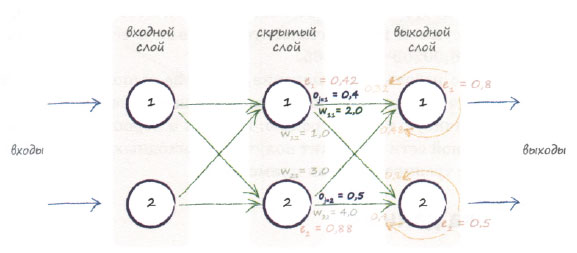
Мы хотим обновить весовой коэффициент w₁₁ для связи между скрытым и выходным слоями, текущее значение которого равно 2,0. Запишем еще раз выражение для градиента ошибки.

Разберем это выражение по частям.

Первая часть (t_k - o_k) - это уже известная вам по предыдущим диаграммам ошибка e₁ = 0,8.
Сумма Σ_jw_jko_j, передаваемая сигмоидам, равна (2,0 * 0,4) + (3,0 * 0,5) = 2,3.
Тогда сигмоида 1 / (1 + е^-2,3) равна 0,909. Следовательно, промежуточное выражение равно 0,909 * (1 - 0,909) = 0,083.
Последняя часть - это просто сигнал о_j, которым в данном случае является сигнал о_j=1, так как нас интересует вес w₁₁, где j = l. Поэтому данная часть просто равна 0,4.

Перемножив все три части этого выражения и не забыв при этом о начальном знаке "минус", получаем значение -0,0265.

При коэффициенте обучения, равном 0,1, изменение веса составит -0,1 * (-0,0265) = +0,002650. Следовательно, новое значение w₁₁, определяемое суммой первоначального значения и его изменения, составит 2,0 + 0,00265 = 2,00265.

Это довольно небольшое изменение, но после выполнения сотен или даже тысяч итераций весовые коэффициенты в конечном счете образуют устойчивую конфигурацию, которая в хорошо натренированной нейронной сети обеспечит получение выходных сигналов, согласующихся с тренировочными примерами.

Со следующего шага мы начнем знакомиться с подготовкой данных.

Предыдущий шаг Содержание Следующий шаг