На этом шаге мы рассмотрим проблемы, возникающие при выполнении декомпозиции задач.
Следующий шаг рекурсивной методики состоит в выявлении подзадач, подобных, но меньших исходной (и, возможно, других разнообразных задач), как показано на рисунке 1 4 шага. Эти меньшие подзадачи будут использоваться на шаге 4 шаблона проектирования для определения рекурсивных условий. Процесс заключается в уменьшении размера задачи с целью определить её меньшие экземпляры и тем самым приблизить её к начальным условиям. Поэтому перед продолжением этого шага важно правильно установить размер задачи и ее начальные условия.
Многие рекурсивные решения уменьшают размер задачи на 1 или делят его надвое. Представление задач в виде схем полезно и очень рекомендуется, так как они помогают наглядно распознать подобные исходной подзадачи, то есть рекурсию, и могут также облегчить определение рекурсивных условий. На рисунке 1 приведены дополнительные схемы, иллюстрирующие декомпозицию задачи суммирования первых положительных целых чисел, когда размер задачи уменьшается на 1.

Рис.1. Дополнительные схемы, иллюстрирующие декомпозицию суммы первых n положительных целых чисел с уменьшением размера задачи на единицу
Во-первых, поскольку рекурсия - это математическая функция, которая может быть выражена формулой, мы можем просто развернуть выражение так, чтобы идентифицировать исходную задачу и соответствующую подзадачу, как показано на рис. 1(a). На рис. 1(b) схема также содержит формулу, но использует вместо фигурных скобок поля, заключающие формулы. В этом случае более темный внешний блок представляет полную задачу, тогда как вложенный в него более светлый блок обозначает подзадачу. Схема на рис. 1(c) подобна схеме на рис. 1(b), но задача состоит в добавлении кружочков, выстроенных треугольником. Наконец, на рис. 1(d), чтобы показать задачу и подзадачу, суммируемые числа размещены в сопоставимых друг с другом прямоугольниках.
Эти довольно простые схемы целесообразны, поскольку позволяют обнаружить подзадачу внутри исходной задачи. При этом крайне важно подчеркнуть, что подзадача уже не делится на более мелкие. Например, сумма n - 2 положительных целых чисел не появляется явно как подзадача ни в одной из схем. Иными словами, схемы не должны показывать вложенность или древовидность подзадач. В этом - одна из основных ловушек рекурсивного подхода, а также источник недоразумений. На рис. 2(a) и 2(c) показаны правильные декомпозиции задачи суммирования первых n положительных целых чисел (S(n)).

Рис.2. При рекурсивном подходе обычно нет нужды представлять декомпозицию задачи всеми её экземплярами меньшего размера
Напротив, хотя вложенные подзадачи на рис. 2(b) или (унарное) дерево рекурсивных вызовов на рис. 2(d) правильно отражают задачу, они содержат дополнительные подзадачи (S(1), S(2), ..., S(n - 2)), которых нет в рекурсивном определении (1.5). Поэтому такие подзадачи во избежание путаницы должны удаляться из схем и, следовательно, из самого рекурсивного процесса. Тем не менее вложенные и древовидные схемы могут быть полезными для других задач.
Стремление избежать вложенных схем не означает, что необходимо рассматривать только одну подзадачу. Многие рекурсивные определения требуют разложения исходной задачи на множество подзадач. Например, на рис. 3 приведены две схемы декомпозиции функции Фибоначчи. В частности, вариант (a) соответствует определению (1.2), а вариант (b) - определению (1.7). Несмотря на то что в схеме (b) показаны все подзадачи от F(1) до F(n - 2), такое представление допустимо, так как эти подзадачи не являются вложенными.
В большинстве задач размер будет зависеть только от одного параметра или фактора, но в некоторых он будет зависеть от нескольких параметров. Например, матричные задачи обычно зависят от высоты (количества строк) и ширины (количества столбцов) матрицы. Поэтому задачи меньшего размера могут стать результатом уменьшения одного или обоих из этих параметров. В частности, многие рекурсивные алгоритмы делят матрицы на блоки - подматрицы. Такие "блочные матрицы" можно интерпретировать как исходную матрицу с вертикальными и горизонтальными разделителями, как показано в следующем примере с матрицей размером 4х7:
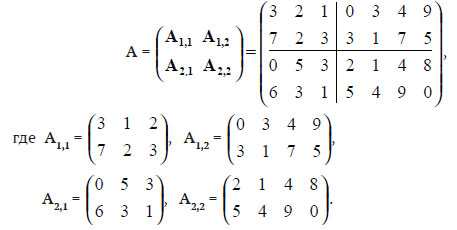
Здесь число строк и столбцов каждой подматрицы получено целочисленным делением на два исходных высоты и ширины матрицы.
Что касается эффективности метода деления размера задачи пополам, то он может приводить к более быстрым алгоритмам, чем постепенное уменьшение размера на 1. Поэтому такую стратегию нужно иметь в виду вообще и в особенности тогда, когда теория показывает возможное снижение стоимости вычислений алгоритма по сравнению с уменьшением размера задачи на единицу. Однако деление размера задачи пополам не всегда приводит к приемлемому рекурсивному алгоритму. Например, трудно получить простую рекурсивную формулу для функции n! с использованием подзадачи (n/2)!.
На следующем шаге мы начнем рассматривать рекурсивные условия, индукция и схемы.
